Question

设等差数列{a_n}的前n项和为S_n，满足a₃+a₅=26，S₉=153，递增的等比数列{b_n}中，满足b₂•b₅=128．
（Ⅰ）求数列{a_n}、{b_n}的通项公式；
（Ⅱ）设?x∈N^*，试比较S_n，b_n的大小．

Answer 1

考点：等差数列与等比数列的综合

专题：等差数列与等比数列

分析：（Ⅰ）根据等差数列和等比数列的定义求出相应的首项和公差，公比，即可求数列{a_n}、{b_n}的通项公式；
（Ⅱ）求出S_n，b_n的表达式，利用函数图象进行比较大小．

解答： 解：（I）由题意得：在等差数列{a_n}中，a₃+a₅=26⇒a₁+3d=26…①
S9=

9×(a1+a9)

2

=9a1+36d=153…②；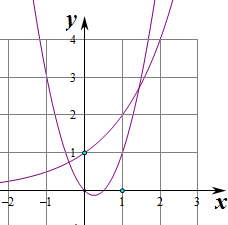
联立①②解出a₁=1，d=4，
∴a_n=1+4（n-1）=4n-3；
在数列{b_n}中，

b2×b5=128 b1+b6=66

⇒

b1=64 b6=2

或

b1=2 b6=64

．
∵{b_n}是递增数列；
∴b₁=2，b₆=64，而b6=b1•q5⇒q=2；
∴bn=2•2n-1=2n(n∈N*)
∴数列{a_n}的通项公式为an=4n-3，(n∈N*)；{b_n}通项公式为bn=2n(n∈N*)．
 （II）由（I）得Sn=

n(4n-2)

2

=2n2-n，(n∈N*)，而bn=2n，
图象如右所示：
显然①当S_n＞b_n时，n=2，3，4，5，6，
∴S_n＞b_n．
②S_n＜b_n时，n=1或n≥7，
∴S_n＜b_n．

点评：本题主要考查等差数列和等比数列的通项公式的计算，根据条件建立方程解方程即可得到结论．