题目内容

5．若复数z满足$\frac{z+2i}{z}$=2+3i，其中i为虚数单位，则z=（　　）
A．$\frac{2}{5}$+$\frac{3}{5}$iB．$\frac{3}{5}$+$\frac{2}{5}$iC．$\frac{3}{5}$+$\frac{1}{5}$iD．$\frac{1}{5}$+$\frac{3}{5}$i

分析 把已知的等式变形，然后利用复数代数形式的乘除运算化简得答案．

解答 解：由$\frac{z+2i}{z}$=2+3i，得z+2i=z（2+3i），
即2i=z（1+3i），
∴$z=\frac{2i}{1+3i}=\frac{2i（1-3i）}{（1+3i）（1-3i）}=\frac{3}{5}+\frac{1}{5}i$．
故选：C．

点评 本题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础题．

练习册系列答案
相关题目
15．对于函数f（x），g（x）满足：对任意x∈R，都有f（x2-2x+3）=g（x），若关于x的方程g（x）+sin$\frac{π}{2}$x=0只有5个根，则这5个根之和为（　　）
A．5B．6C．8D．9
16．有三对师徒共6个人，站成一排照相，每对师徒相邻的站法共有（　　）
A．72B．54C．48D．8
13．一几何体的三视图是如图所示的三个直角边为2的等腰直角三角形，则该几何体的表面积为（　　）
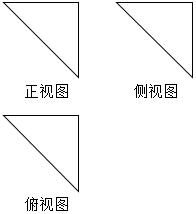
A．8B．4$\sqrt{3}$+4C．4$\sqrt{2}$+4D．6+2$\sqrt{3}$
20．设定义域为R的函数f（x）=$\left\{\begin{array}{l}{{2}^{-|x-2|}+1（x≠2）}\\{a（x=2）}\end{array}\right.$，若关于x的方程2f2（x）-（2a+3）f（x）+3a=0有五个不同的实数解，则a的取值范围是（1，$\frac{3}{2}$）∪（$\frac{3}{2}$，2）．
10．已知数列{an}为等差数列，若a1，a2，a3成等比数列，且a1=1，则公差d=（　　）
A．0B．1C．2D．4
17．已知函数$f（x）=\left\{{\begin{array}{l}{x+\frac{1}{x}+a，x＞0}\\{{2^x}+a，x≤0}\end{array}}\right.$，若方程f（x）=-x有且仅有一解，则实数a的取值范围为a≥-1或a=-2$\sqrt{2}$．．
14．设a∈R，则“a＞1”是“a2＞|a-2|”的（　　）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件
15．函数y=2x2+4x+1（x≤-2）的反函数是y=-1-$\sqrt{\frac{x+1}{2}}$，（x≥1）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网