题目内容
20.设定义域为R的函数f(x)=$\left\{\begin{array}{l}{{2}^{-|x-2|}+1(x≠2)}\\{a(x=2)}\end{array}\right.$,若关于x的方程2f2(x)-(2a+3)f(x)+3a=0有五个不同的实数解,则a的取值范围是(1,$\frac{3}{2}$)∪($\frac{3}{2}$,2).分析 作出函数f(x)的图象,利用换元法转化为一元二次方程根的分布情况,利用数形结合是解决本题的关键.
解答 解:作出函数f(x)的图象如图: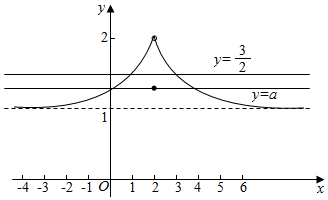
设t=f(x),则方程2f2(x)-(2a+3)f(x)+3a=0等价为2t2-(2a+3)t+3a=0,即(t-a)(2t-3)=0,
得t=$\frac{3}{2}$或t=a,
当t=$\frac{3}{2}$时,f(x)=t=$\frac{3}{2}$此时有两个根,
要使方程2f2(x)-(2a+3)f(x)+3a=0有五个不同的实数解,
则等价为f(x)=a,有三个不同的根,
即1<a<2,且a≠$\frac{3}{2}$,
即a的取值范围是(1,$\frac{3}{2}$)∪($\frac{3}{2}$,2),
故答案为:(1,$\frac{3}{2}$)∪($\frac{3}{2}$,2).
点评 本题主要考查函数与方程的应用,利用换元法转化为一元二次方程根的情况,利用数形结合以及分类讨论是解决本题的关键,综合性较强,有一定的难度.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
5.若复数z满足$\frac{z+2i}{z}$=2+3i,其中i为虚数单位,则z=( )
| A. | $\frac{2}{5}$+$\frac{3}{5}$i | B. | $\frac{3}{5}$+$\frac{2}{5}$i | C. | $\frac{3}{5}$+$\frac{1}{5}$i | D. | $\frac{1}{5}$+$\frac{3}{5}$i |
