题目内容
19.设b,c分别是先后抛掷一枚骰子得到的点数.(1)设A={x|x2-bx+2c<0,x∈R},求A≠∅的概率;
(2)设随机变量ξ=|b-c|,求ξ的分布列.
分析 (1)由A≠∅,知△=b2-8c>0,由此利用列举法能求出A≠∅的概率.
(2)由题意得ξ的可能取值为0,1,2,3,4,5,分别求出相应的概率,由此能求出ξ的分布列.
解答 解:(1)设f(x)=x2-bx+2c,
由A≠∅,知△=b2-8c>0.
又b,c∈{1,2,3,4,5,6}
所以b=6时,c=1,2,3,4;
b=5时,c=1,2,3;
b=4时,c=1;
b=3时,c=1.
由于f(x)随b,c取值变化,有6×6=36个
故所求的概率为P=$\frac{9}{6×6}=\frac{1}{4}$.
(2)由题意得ξ的可能取值为0,1,2,3,4,5,
P(ξ=0)=$\frac{6}{36}=\frac{1}{6}$,
P(ξ=1)=$\frac{10}{36}=\frac{5}{18}$,
P(ξ=2)=$\frac{8}{36}=\frac{2}{9}$,
P(ξ=3)=$\frac{6}{36}=\frac{1}{6}$,
p(ξ=4)=$\frac{4}{36}=\frac{1}{9}$,
p(ξ=5)=$\frac{2}{36}=\frac{1}{18}$,
∴ξ的分布列为:
| P | 0 | 1 | 2 | 3 | 4 |
| ξ | $\frac{1}{6}$ | $\frac{5}{18}$ | $\frac{2}{9}$ | $\frac{1}{6}$ | $\frac{1}{9}$ |
点评 本小题主要概率、离散型随机变量的分布列等基础知识,考查数据处理能力、运算求解能力以及应用意识,考查必然与或然思想等,是中档题.

练习册系列答案
相关题目
14.定义A*B,B*A,C*D,D*A的运算分别对应图2中的(1)(2)(3)(4),那么,图1中(A)(B)可能是下列的运算的结果( )
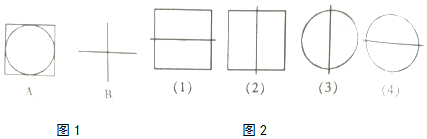

| A. | B*D,A*D | B. | B*D,A*C | C. | B*C,A*D | D. | C*D,A*D |
 如图,四边形BCDE是直角梯形,CD∥BE,CD丄BC,CD=$\frac{1}{2}$BE=2,平面BCDE丄平面ABC,又已知△ABC为等腰直角三角形,AB=AC=4,M是BC的中点.
如图,四边形BCDE是直角梯形,CD∥BE,CD丄BC,CD=$\frac{1}{2}$BE=2,平面BCDE丄平面ABC,又已知△ABC为等腰直角三角形,AB=AC=4,M是BC的中点.