题目内容
4.某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:①sin213°+cos217°-sin13°cos17°;
②sin215°+cos215°-sin15°cos15°;
③sin218°+cos212°-sin18°cos12°;
④sin2(-18°)+cos248°-sin(-18°)cos48°
⑤sin2(-25°)+cos255°-sin(-25°)cos55°(1)试从上述五个式子中选择一个,求出这个常数;
(2)根据(1)的计算结果,将该同学的发现推广为一三角恒等式,并证明你的结论.
(参考公式:sin(α±β)=sinαcosβ±cosαsinβ,cos(α±β)=cosαcosβ?sinαsinβsin2α=2sinαcosα,cos2α=cos2α-sin2α=2cos2α-1=1-2sin2α)
分析 (1)选择②式由sin215°+cos215°-sin15°cos15°=1-$\frac{1}{2}sin30°$=$\frac{3}{4}$,可得这个常数的值.
(2)推广,得到三角恒等式sin2α+cos2(30°-α)-sinαcos(30°-α)=$\frac{3}{4}$,直接利用两角差的余弦公式代入等式的左边,化简可得结果.
解答 解:(1)选择②式,计算如下:sin215°+cos215°-sin15°cos15°=1-$\frac{1}{2}sin30°$=$\frac{3}{4}$;------(4分),
(2)三角恒等式为sin2α+cos2(30°-α)-sinαcos(30°-α)=$\frac{3}{4}$,---(6分)
证明如下:sin2α+cos2(30°-α)-sinαcos(30°-α)=sin2α+(cos30°cosα+sin30°sinα)2-sinα(cos30°cosα+sin30°sinα)---(7分),
=sin2α+($\frac{\sqrt{3}}{2}$cosα+$\frac{1}{2}$sinα)2-sinα($\frac{\sqrt{3}}{2}$cosα+$\frac{1}{2}$sinα)=$\frac{3}{4}$sin2α+$\frac{3}{4}$cos2α=$\frac{3}{4}$---(12分),
点评 本题主要考查两角差的余弦公式,二倍角公式的应用,考查归纳推理以及计算能力,属于中档题.

练习册系列答案
相关题目
14.圆心在x轴上,半径长为 $\sqrt{2}$,且过点(-2,1)的圆的方程为( )
| A. | (x+1)2+y2=2 | B. | x2+(y+2)2=2 | ||
| C. | (x+3)2+y2=2 | D. | (x+1)2+y2=2或(x+3)2+y2=2 |
16.函数y=cos(2x+φ)(-π≤φ≤π)的图象向右平移$\frac{π}{2}$个单位后与函数$y=sin(2x+\frac{π}{3})$的图象重合,此时φ=( )
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $-\frac{π}{6}$ |
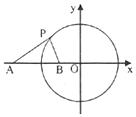 已知圆C:x2+y2=9,点A(-5,0),直线l:x-2y=0.
已知圆C:x2+y2=9,点A(-5,0),直线l:x-2y=0.