题目内容
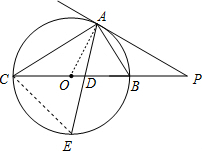
如图所示，PA为圆O的切线，A为切点，PO交于圆O与B，C两点，PA=10，PB=5，∠BAC的角平分线与BC和圆O分别交于点D和E．（Ⅰ）求
| AB |
| AC |
| PA |
| PC |
（Ⅱ）求AD•AE的值．
考点：与圆有关的比例线段,相似三角形的性质
专题：选作题,立体几何
分析：（Ⅰ）证明△PAB∽△PCA，可得
=
；
（Ⅱ）由切割线定理求出PC=40，BC=30，由已知条件条件推导出△ACE∽△ADB，由此能求出AD•AE的值．
| AB |
| AC |
| PA |
| PC |
（Ⅱ）由切割线定理求出PC=40，BC=30，由已知条件条件推导出△ACE∽△ADB，由此能求出AD•AE的值．
解答：
解：（Ⅰ）∵PA为圆O的切线，
∴∠PAB=∠ACP，又∠P为公共角，
∴△PAB∽△PCA，
∴
=
．…（4分）
（Ⅱ）∵PA为圆O的切线，BC是过点O的割线，
∴PA2=PB•PC，
∴PC=20，BC=15，
又∵∠CAB=90°，∴AC2+AB2=BC2=225，
又由（Ⅰ）知
=
=
，∴AC=6
AB=3
，
连接EC，则∠CAE=∠EAB，
∴△ACE∽△ADB，
∴
=
，
∴AD•AE=AB•AC=3
×6
=90． …（10分）
解：（Ⅰ）∵PA为圆O的切线，∴∠PAB=∠ACP，又∠P为公共角，
∴△PAB∽△PCA，
∴
| AB |
| AC |
| PA |
| PC |
（Ⅱ）∵PA为圆O的切线，BC是过点O的割线，
∴PA2=PB•PC，
∴PC=20，BC=15，
又∵∠CAB=90°，∴AC2+AB2=BC2=225，
又由（Ⅰ）知
| AB |
| AC |
| PA |
| PC |
| 1 |
| 2 |
| 5 |
| 5 |
连接EC，则∠CAE=∠EAB，
∴△ACE∽△ADB，
∴
| AB |
| AE |
| AD |
| AC |
∴AD•AE=AB•AC=3
| 5 |
| 5 |
点评：本题考查了切线的性质，相似三角形的性质和判定，等腰三角形的性质，圆周角定理等知识点的应用．
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
如果直线ax+by=4与圆C：x2+y2=4相离，那么点P（a，b）与圆C的位置关系是（ ）
| A、在圆内 | B、在圆上 |
| C、在圆外 | D、不确定 |
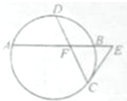如图，已知圆中两条弦AB与CD相交于点F，且DF=CF=