题目内容
设函数f（x）=（m-3）ex，g（x）=2ax+1+blnx，其中m，a，b∈R，曲线g（x）在x=1处的切线方程为y=3x．
（1）求函数g（x）的解析式；
（2）若f（x）的图象恒在g（x）图象的上方，求m的取值范围；
（3）讨论关于x的方程f（x）=g（x）根的个数．
（1）求函数g（x）的解析式；
（2）若f（x）的图象恒在g（x）图象的上方，求m的取值范围；
（3）讨论关于x的方程f（x）=g（x）根的个数．
考点：利用导数求闭区间上函数的最值,利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：（1）由导数的几何意义求得a，b的值即可得出结论；
（2）由题意，（m-3）ex＞2x+1+lnx对一切x＞0恒成立，分离参数m得m＞
+3，令h(x)=
+3，
利用导数求得h（x）的最大值，即可得出结论．
（3）由题意，原方程等价于分离参数后的方程m=
+3，令h(x)=
+3，利用导数判断函数的单调性，数形结合即可得出结论．
（2）由题意，（m-3）ex＞2x+1+lnx对一切x＞0恒成立，分离参数m得m＞
| 2x+1+lnx |
| ex |
| 2x+1+lnx |
| ex |
利用导数求得h（x）的最大值，即可得出结论．
（3）由题意，原方程等价于分离参数后的方程m=
| 2x+1+lnx |
| ex |
| 2x+1+lnx |
| ex |
解答：
解：（1）g′(x)=2a+
，则g'（1）=2a+b=3，又g（1）=2a+1=3，
解得a=1，b=1，所以g（x）=2x+1+lnx．
（2）由题意，（m-3）ex＞2x+1+lnx对一切x＞0恒成立，
分离参数m得m＞
+3，
令h(x)=
+3，则h′(x)=
，
令t(x)=1+
-2x-lnx，探根：令x=1，则t（1）=0，
又t′(x)=-
-2-
＜0，说明函数t（x）过点（1，0），且在（0，+∞）上单调递减，
其大致图象如图．
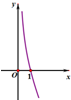
观察图象即知，当x∈（0，1）时，t（x）＞0；当x∈（1，+∞）时，t（x）＜0．
又易知h'（x）与t（x）同号，所以h（x）在（0，1）上单调递增；在（1，+∞）上单调递减，
即hmax(x)=h(1)=
+3，故所求m取值范围为(
+3， +∞)．
（3）由题意，原方程等价于分离参数后的方程m=
+3，
仍令h(x)=
+3，则由（1）知：h（x）在（0，1）上单调递增；在（1，+∞）上单调递减．
又当x→0+时，h（x）→-∞；当x→+∞时，h（x）→3，即直线x=0（y轴）和y=3是函数h（x）图象的两条渐近线，
所以h（x）的大致图象如图2，观察图象即知：
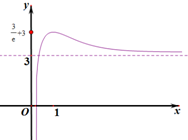
当m=
+3或m∈（-∞，3]时，方程f（x）=g（x）根的个数为1；
当m∈（3，
+3）时，f（x）=g（x）根的个数为2；
当m∈（
+3，+∞）时，f（x）=g（x）根的个数为0．
| b |
| x |
解得a=1，b=1，所以g（x）=2x+1+lnx．
（2）由题意，（m-3）ex＞2x+1+lnx对一切x＞0恒成立，
分离参数m得m＞
| 2x+1+lnx |
| ex |
令h(x)=
| 2x+1+lnx |
| ex |
1+
| ||
| ex |
令t(x)=1+
| 1 |
| x |
又t′(x)=-
| 1 |
| x2 |
| 1 |
| x |
其大致图象如图．
观察图象即知，当x∈（0，1）时，t（x）＞0；当x∈（1，+∞）时，t（x）＜0．
又易知h'（x）与t（x）同号，所以h（x）在（0，1）上单调递增；在（1，+∞）上单调递减，
即hmax(x)=h(1)=
| 3 |
| e |
| 3 |
| e |
（3）由题意，原方程等价于分离参数后的方程m=
| 2x+1+lnx |
| ex |
仍令h(x)=
| 2x+1+lnx |
| ex |
又当x→0+时，h（x）→-∞；当x→+∞时，h（x）→3，即直线x=0（y轴）和y=3是函数h（x）图象的两条渐近线，
所以h（x）的大致图象如图2，观察图象即知：
当m=
| 3 |
| e |
当m∈（3，
| 3 |
| e |
当m∈（
| 3 |
| e |
点评：本题主要考查利用导数研究函数的切线问题，研究函数的单调性、最值等知识，考查学生转化划归思想、分类讨论思想的运用能力及分析问题、解决问题的能力，属难题．
练习册系列答案
相关题目
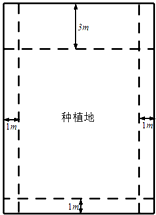某部队驻扎在青藏高原上，那里海拔高、寒冷缺氧、四季风沙、没有新鲜蔬菜，生活条件极为艰苦．但战士们不计个人得失，扎根风雪高原，以钢铁般的意志，自力更生，克服恶劣的自然环境．该部队现计划建造一个室内面积为800m2的矩形蔬菜温室，在温室内，与左、右两侧及后侧的内墙各保留1m宽的通道，与前侧内墙保留3m宽的空地．当矩形温室的边长各为多少时，蔬菜的种植面积最大？最大种植面积是多少？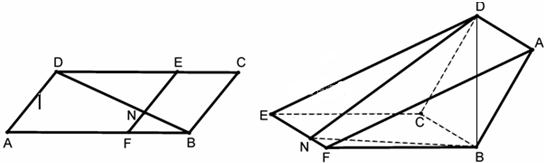
如图在四棱锥P-ABCD中，底面ABCD是边长为a的正方形，侧面PAD⊥底面ABCD，且PA=PD=