题目内容
8.已知3sin2α-2sinα+2sin2β=0,试求sin2α+sin2β的取值范围.分析 由3sin2α-2sinα+2sin2β=0,可得sin2β=sinα-$\frac{3}{2}$sin2α,带入sin2α+sin2β转换为二次函数问题求解即可.
解答 解:由3sin2α-2sinα+2sin2β=0,可得sin2β=sinα-$\frac{3}{2}$sin2α,
∵sin2β≥0,即sinα-$\frac{3}{2}$sin2α≥0,
可得:0≤sinα$≤\frac{2}{3}$
那么:sin2α+sin2β=sinα-$\frac{1}{2}$sin2α=$-\frac{1}{2}$(sin2α-2sinα+1)+$\frac{1}{2}$=$-\frac{1}{2}$(sinα-1)2$+\frac{1}{2}$.
∴当sinα=0时,sin2α+sin2β取得最小值为0.
当sinα=$\frac{2}{3}$时,sin2α+sin2β取得最大值为$\frac{4}{9}$.
∴sin2α+sin2β的取值范围是[0,$\frac{4}{9}$].
点评 本题主要考查了三角函数的有界限的运用和二次函数的运用,求出sinα的范围是解题的关键.属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.空间中两点A(3,-2,5),B(6,0,-1)之间的距离为( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
19.下面四个推理不是合情推理的是( )
| A. | 由圆的性质类比推出球的有关性质 | |
| B. | 由直角三角形、等腰三角形、等边三角形的内角和都是180°,归纳出所有三角形的内角和都是180° | |
| C. | 某次考试张军的成绩是100分,由此推出全班同学的成绩都是100分 | |
| D. | 蛇、海龟、蜥蜴是用肺呼吸的,蛇、海龟、蜥蜴是爬行动物,所以所有的爬行动物都是用肺呼吸的 |
13.已知函数y=sin(2x+φ)+1的图象关于直线$x=-\frac{π}{8}$对称,则φ的可能取值是( )
| A. | $\frac{3π}{4}$ | B. | $-\frac{3π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
20.下列说法正确的是( )
| A. | “sinα=$\frac{3}{5}$”是“cos2α=$\frac{7}{25}$”的必要不充分条件 | |
| B. | 命题“若xy=0,则x=0或y=0”的否命题是“若xy≠0,则x≠0或y≠0” | |
| C. | 已知命题p:?x∈R,使2x>3x;命题q:?x∈(0,+∞),都有$\frac{1}{{x}^{2}}$<$\frac{1}{{x}^{3}}$,则p∧(¬q)是真命题 | |
| D. | 从匀速传递的生产流水线上,质检员每隔5分钟从中抽取一件产品进行某项指标检测,这是分层抽样 |
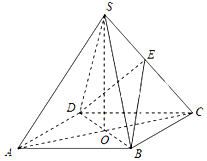 如图,在四棱锥S-ABCD中,底面ABCD是正方形,其他四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC的中点.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,其他四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC的中点.