题目内容
17.已知$|{sin2α}|=\frac{24}{25}$,且$\frac{3π}{4}<α<π$,则tanα=$\frac{3}{4}$.分析 利用sin2α=$\frac{2sinαcosα}{si{n}^{2}α+co{s}^{2}α}=\frac{2tanα}{ta{n}^{2}α+1}$,结合已知条件可得sin2α,cos2α的值,再由倍角公式求出sinα,cosα,则tanα的值可求.
解答 解:sin2α=$\frac{2sinαcosα}{si{n}^{2}α+co{s}^{2}α}=\frac{2tanα}{ta{n}^{2}α+1}$,
∵$|{sin2α}|=\frac{24}{25}$,
∴sin2α=$±\frac{24}{25}$.
∵$\frac{3π}{4}$<α<π,∴$\frac{3π}{2}$<2α<2π.
∴sin2α=$-\frac{24}{25}$,cos2α=$\frac{7}{25}$.
∵1-2sin2α=$\frac{7}{25}$,
∴sin2α=$\frac{9}{25}$.
又$\frac{3π}{4}$<α<π,
∴sinα=$-\frac{3}{5}$,cosα=-$\frac{4}{5}$.
则tanα=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题考查了倍角公式、同角三角函数基本关系式、三角函数值与角所在象限的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
7.已知复数z1=-2-i,z2=i,i是虚数单位,则复数z1-2z2的值是( )
| A. | -1+2i | B. | 1-2i | C. | 1+2i | D. | -2-3i |
2.如果曲线y=f(x)在点(2,3)处的切线过点(-1,2),则有( )
| A. | f′(2)<0 | B. | f′(2)=0 | C. | f′(2)>0 | D. | f′(2)不存在 |
9.化简sin(x+y)sinx+cos(x+y)cosx等于( )
| A. | cos(2x+y) | B. | cosy | C. | sin(2x+y) | D. | siny |
6.化简sin690°的值是( )
| A. | 0.5 | B. | -0.5 | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
7.已知三条不重合的直线m,n,l 和两个不重合的平面 α,β 下列命题正确的是( )
| A. | 若m∥n,n?α,则 m∥α | B. | 若α⊥β,α∩β=m,m⊥n,则 n⊥α | ||
| C. | 若l⊥n,m⊥n,则 l∥m | D. | 若l⊥α,m⊥β,且 l⊥m,则 α⊥β |
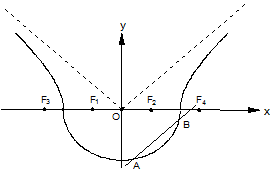 如图,曲线Г由曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≤0)和曲线C2:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y>0)组成,其中点F1,F2为曲线C1所在圆锥曲线的焦点,点F3,F4为曲线C2所在圆锥曲线的焦点,
如图,曲线Г由曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≤0)和曲线C2:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y>0)组成,其中点F1,F2为曲线C1所在圆锥曲线的焦点,点F3,F4为曲线C2所在圆锥曲线的焦点,