题目内容
8.已知α∈(0,$\frac{π}{2}$),且tan(α+$\frac{π}{4}$)=3,则lg(8sinα+6cosα)-lg(4sinα-cosα)=1.分析 根据角的范围,由两角和的正切函数公式可求tanα,利用对数的运算性质即可计算得解.
解答 解:∵α∈(0,$\frac{π}{2}$),且tan(α+$\frac{π}{4}$)=3,
∴$\frac{tanα+1}{1-tanα}$=3,
∴tan$α=\frac{1}{2}$,
∴lg(8sinα+6cosα)-lg(4sinα-cosα)=lg$\frac{8sinα+6cosα}{4sinα-cosα}$=lg$\frac{8tanα+6}{4tanα-1}$=lg10=1.
故答案为:1.
点评 本题主要考查了两角和的正切函数公式,对数的运算性质,考查了计算能力,属于基础题.

练习册系列答案
相关题目
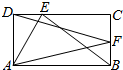
18.如图E,F在边长分别为2和1的矩形边DC与BC上,若$\overrightarrow{AE}•\overrightarrow{AF}$=6,则$\overrightarrow{BE}•(\overrightarrow{DF}+\overrightarrow{AF})$等于( )

| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
19.函数$f(x)=\frac{{|{2-x}|}}{{\sqrt{x+2}}}-{(x-\frac{3}{2})^0}$的定义域是( )
| A. | $(-2,\frac{3}{2})∪(\frac{3}{2},+∞)$ | B. | $(-2,\frac{3}{2})$ | C. | $(\frac{3}{2},+∞)$ | D. | (-2,+∞) |
16.在三棱锥P一ABC中,PA⊥平面ABC,△ABC为边长为2的正三角形,PA=$\sqrt{3}$,则AP与平面PBC所成的角为( )
| A. | 45° | B. | 60° | C. | 75° | D. | 90° |
13.设函数f(x)=-x3+bx(b为常数),若方程f(x)=0的根都在区间[-2,2]内,且函数f(x)在区间(0,1)上单调递增,则b的取值范围是( )
| A. | [3,+∞) | B. | (3,4] | C. | [3,4] | D. | (-∞,4] |
20.在△ABC中,角A,B,C所对的边分别为a,b,c,其中c=3,$a=3\sqrt{2}$,$cosB=\frac{{\sqrt{2}}}{4}$,则sinA=( )
| A. | $\frac{7}{24}$ | B. | $\frac{{3\sqrt{7}}}{8}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{14}}}{4}$ |
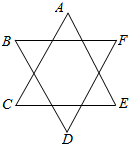 用4种不同的颜色对图中A,B,C,D,E,F六个点进行染色,要求同一线段的两点(如:AC,BD,…)颜色不相同,而且相邻的两点(如:AB,BC,…)颜色也不相同,则不同的染色方案种数为96 (用数学作答).
用4种不同的颜色对图中A,B,C,D,E,F六个点进行染色,要求同一线段的两点(如:AC,BD,…)颜色不相同,而且相邻的两点(如:AB,BC,…)颜色也不相同,则不同的染色方案种数为96 (用数学作答).