题目内容
如图,圆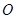 与离心率为
与离心率为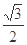 的椭圆
的椭圆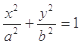 (
(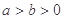 )相切于点
)相切于点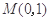 .
.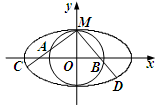
(Ⅰ)求椭圆的方程;
(Ⅱ)过点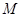 引两条互相垂直的两直线
引两条互相垂直的两直线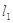 、
、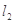 与两曲线分别交于点
与两曲线分别交于点 、
、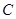 与点
与点 、
、 (均不重合).
(均不重合).
(ⅰ)若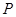 为椭圆上任一点,记点
为椭圆上任一点,记点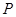 到两直线的距离分别为
到两直线的距离分别为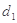 、
、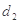 ,求
,求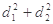 的最大值;
的最大值;
(ⅱ)若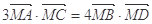 ,求
,求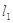 与
与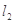 的方程.
的方程.
(Ⅰ)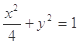 。
。
(Ⅱ) 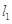 的方程为
的方程为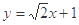 ,
,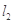 的方程为
的方程为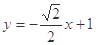
或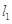 的方程为
的方程为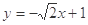 ,
,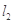 的方程为
的方程为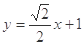 。
。
解析试题分析:(Ⅰ)由题意: 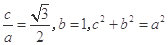 解得
解得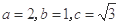 2分
2分
椭圆的方程为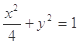 3分
3分
(Ⅱ)(ⅰ)设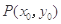 因为
因为 ⊥
⊥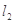 ,则
,则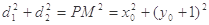 因为
因为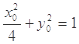
所以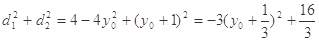 5分
5分
因为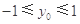
所以当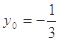 时
时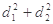 取得最大值为
取得最大值为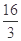 ,此时点
,此时点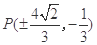 6分
6分
(ⅱ)设 的方程为
的方程为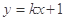 ,由
,由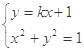 解得
解得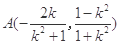
由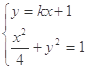 解得
解得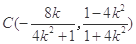 8分
8分
同理可得 ,
,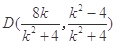 10分
10分
所以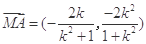 ,
,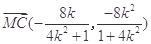
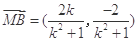 ,
,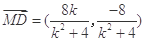
由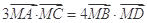 得
得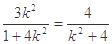 解得
解得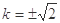 13分
13分
所以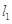 的方程为
的方程为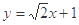 ,
,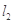 的方程为
的方程为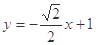
或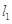 的方程为
的方程为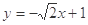 ,
,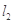 的方程为
的方程为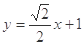 14分
14分
考点:本题主要考椭圆的标准方程,椭圆的几何性质,直线椭圆的位置关系,圆的切线。
点评:难题,求椭圆的标准方程,主要运用了椭圆的几何性质,a,b,c,e的关系。曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题(2)结合向量的坐标运算,确定得到k的方程,为进一步确定直线方程奠定基础。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知椭圆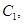
 (a>b>0)抛物线
(a>b>0)抛物线
 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
 | 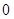 | 4 |  | 1 |
 | 2 | 4 | 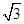 | 2 |
 的标准方程;(2)四边形ABCD的顶点在椭圆
的标准方程;(2)四边形ABCD的顶点在椭圆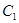 上,且对角线AC、BD过原点O,若
上,且对角线AC、BD过原点O,若 ,
,
(i) 求
 的最值.
的最值.(ii) 求四边形ABCD的面积;
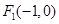 及
及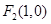 ,点
,点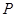 在以
在以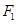 、
、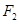 为焦点的椭圆
为焦点的椭圆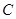 上,且
上,且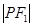 、
、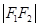 、
、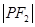 构成等差数列.
构成等差数列.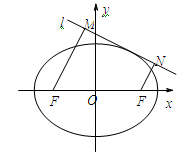
 与椭圆
与椭圆 是直线上的两点,且
是直线上的两点,且 ,
,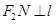 . 求四边形
. 求四边形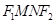 面积
面积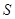 的最大值.
的最大值. 的左、右焦点分别是
的左、右焦点分别是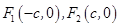 ,Q是椭圆外的动点,满足
,Q是椭圆外的动点,满足 .点
.点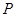 是线段
是线段 与该椭圆的交点,点T是
与该椭圆的交点,点T是 的中点.
的中点.
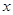 为点
为点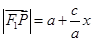 ;
; 的方程.
的方程.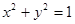 过椭圆
过椭圆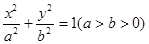 的两焦点,与椭圆有且仅有两个公共点:直线
的两焦点,与椭圆有且仅有两个公共点:直线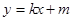 与圆
与圆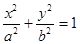 相交于A,B两点记
相交于A,B两点记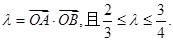
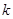 的取值范围;
的取值范围;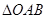 的面积S的取值范围.
的面积S的取值范围. 是直线
是直线 被椭圆
被椭圆 所截得的线段中点,求直线
所截得的线段中点,求直线 的对称轴为坐标轴,焦点是(0,
的对称轴为坐标轴,焦点是(0,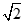 ),(0,
),(0,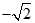 ),又点
),又点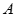
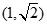 在椭圆
在椭圆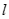 的斜率为
的斜率为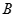 、
、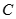 两点,求
两点,求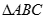 面积的最大值.
面积的最大值.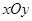 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为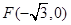 ,右顶点为
,右顶点为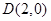 ,设点
,设点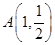 .
. 是椭圆上的动点,求线段
是椭圆上的动点,求线段 中点
中点 的轨迹方程;
的轨迹方程;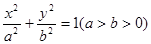 与
与 轴负半轴交于点
轴负半轴交于点 ,
,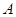 为椭圆第一象限上的点,直线
为椭圆第一象限上的点,直线 交椭圆于另一点
交椭圆于另一点 ,椭圆左焦点为
,椭圆左焦点为 ,连接
,连接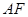 交
交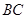 于点D。
于点D。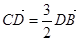 ,求椭圆的离心率;
,求椭圆的离心率; 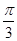 且△ABC的面积为
且△ABC的面积为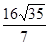 ,求椭圆的标准方程。
,求椭圆的标准方程。