题目内容
已知椭圆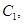
 (a>b>0)抛物线
(a>b>0)抛物线
 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
 | 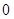 | 4 |  | 1 |
 | 2 | 4 | 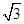 | 2 |
 的标准方程;(2)四边形ABCD的顶点在椭圆
的标准方程;(2)四边形ABCD的顶点在椭圆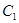 上,且对角线AC、BD过原点O,若
上,且对角线AC、BD过原点O,若 ,
,
(i) 求
 的最值.
的最值.(ii) 求四边形ABCD的面积;
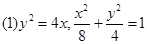
(2)当k=0(此时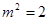 满足①式),即直线AB平行于x轴时,
满足①式),即直线AB平行于x轴时,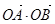 的最小值为-2.
的最小值为-2.
又直线AB的斜率不存在时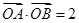 ,所以
,所以 的最大值为2.
的最大值为2.
(ii)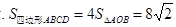 .
.
解析试题分析: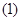
利用待定系数法,将点(0,2),( ,
,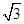 )代入椭圆方程,将(4,4),(1,2)代入抛物线方程,可得
)代入椭圆方程,将(4,4),(1,2)代入抛物线方程,可得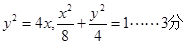
(2)设直线AB的方程为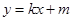 ,设
,设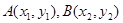
联立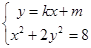 ,得
,得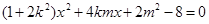
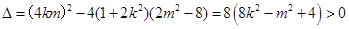 ①
①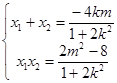
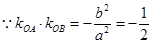


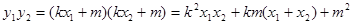
=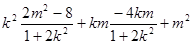
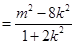
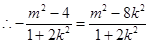

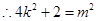
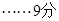
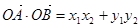
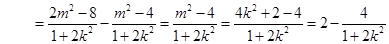
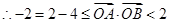
当k=0(此时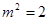 满足①式),即直线AB平行于x轴时,
满足①式),即直线AB平行于x轴时,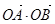 的最小值为-2.
的最小值为-2.
又直线AB的斜率不存在时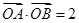 ,所以
,所以 的最大值为2. 11分
的最大值为2. 11分
(ii)设原点到直线AB的距离为d,则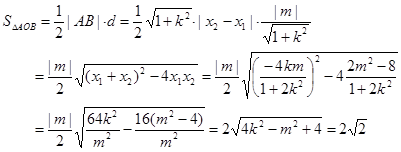
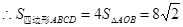 . 13分
. 13分
考点:待定系数法,平面向量的坐标运算,椭圆、抛物线的标准方程,直线与椭圆的位置关系。
点评:中档题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题求椭圆、抛物线的标准方程,主要运用了待定系数法。作为研究图形的面积,涉及弦长公式的应用,利用韦达定理,简化了计算过程。

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
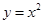 上,A,C关于
上,A,C关于 轴对称,BD平行于抛物线在点C处的切线。
轴对称,BD平行于抛物线在点C处的切线。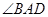 ;
;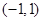 ,四边形ABCD的面积为4,求直线BD的方程。
,四边形ABCD的面积为4,求直线BD的方程。 的圆心为
的圆心为 ,动圆
,动圆 过点
过点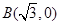 ,且和圆
,且和圆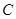 .
.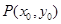 为曲线
为曲线 与曲线
与曲线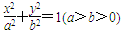 的离心率e为
的离心率e为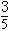 , 且椭圆C的一个焦点与抛物线y2=-12x的焦点重合.
, 且椭圆C的一个焦点与抛物线y2=-12x的焦点重合. -6x+1与坐标轴的交点都在圆C上.
-6x+1与坐标轴的交点都在圆C上.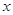 轴上,一个顶点为
轴上,一个顶点为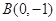 ,且其右焦点到直线
,且其右焦点到直线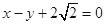 的距离为3.
的距离为3.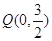 ,与椭圆交于两个不同的点
,与椭圆交于两个不同的点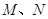 ,且满足
,且满足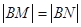 .
.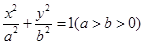 右焦点的直线
右焦点的直线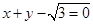 交
交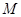 于A,B两点,P为AB的中点,且OP的斜率为
于A,B两点,P为AB的中点,且OP的斜率为 .
.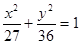 有相同焦点,且经过点
有相同焦点,且经过点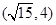 ,求其方程。
,求其方程。 与离心率为
与离心率为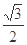 的椭圆
的椭圆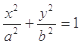 (
(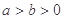 )相切于点
)相切于点 .
.
 引两条互相垂直的两直线
引两条互相垂直的两直线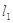 、
、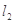 与两曲线分别交于点
与两曲线分别交于点 、
、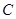 与点
与点 、
、 (均不重合).
(均不重合).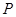 为椭圆上任一点,记点
为椭圆上任一点,记点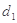 、
、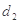 ,求
,求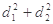 的最大值;
的最大值;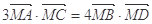 ,求
,求