题目内容
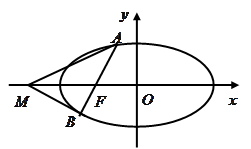
椭圆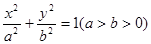 与
与 轴负半轴交于点
轴负半轴交于点 ,
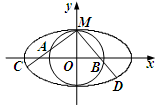
,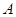 为椭圆第一象限上的点,直线
为椭圆第一象限上的点,直线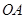 交椭圆于另一点
交椭圆于另一点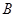 ,椭圆左焦点为
,椭圆左焦点为 ,连接
,连接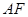 交
交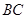 于点D。
于点D。
(1)如果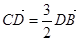 ,求椭圆的离心率;
,求椭圆的离心率;
(2)在(1)的条件下,若直线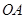 的倾斜角为
的倾斜角为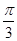 且△ABC的面积为
且△ABC的面积为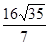 ,求椭圆的标准方程。
,求椭圆的标准方程。
(1) (2)
(2)
解析试题分析:(1)由题意知: 、
、
设 ,
, 则
则
由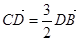 即:
即: 得,
得, 3分
3分
则
由 ,得
,得 ∴
∴ 6分
6分
(2)依题意,可知直线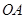 所在直线方程为:
所在直线方程为:
由(1)可知,椭圆方程可化为:
 可得
可得 9分
9分
由面积可得, ,∴
,∴
∴椭圆的标准方程为: 12分
12分
考点:椭圆方程性质及直线与椭圆的位置关系
点评:在求离心率时关键是找到关于 的齐次方程,圆锥曲线中的向量关系式一般都转换为点的坐标运算
的齐次方程,圆锥曲线中的向量关系式一般都转换为点的坐标运算

练习册系列答案
相关题目
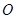 与离心率为
与离心率为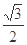 的椭圆
的椭圆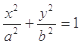 (
(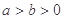 )相切于点
)相切于点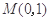 .
.
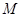 引两条互相垂直的两直线
引两条互相垂直的两直线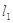 、
、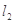 与两曲线分别交于点
与两曲线分别交于点 、
、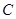 与点
与点 、
、 (均不重合).
(均不重合).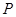 为椭圆上任一点,记点
为椭圆上任一点,记点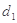 、
、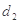 ,求
,求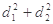 的最大值;
的最大值;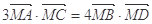 ,求
,求 的中心在原点,焦点在
的中心在原点,焦点在 轴上.若椭圆上的点
轴上.若椭圆上的点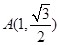 到焦点
到焦点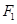 、
、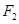 的距离之和等于4.
的距离之和等于4.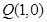 的直线与椭圆交于两点
的直线与椭圆交于两点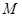 、
、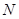 ,当
,当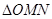 的面积取得最大值时,求直线
的面积取得最大值时,求直线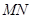 的方程.
的方程.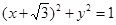 ,
,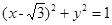 中的一个内切,另一个外切.
中的一个内切,另一个外切.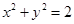 在P(x0,y0)(x0y0 ≠ 0)处的切线,且P在圆上,l与轨迹L相交不同的A,B两点,证明:
在P(x0,y0)(x0y0 ≠ 0)处的切线,且P在圆上,l与轨迹L相交不同的A,B两点,证明: .
.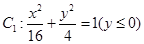 ,曲线
,曲线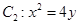 .自曲线
.自曲线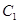 上一点
上一点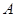 作
作 的两条切线切点分别为
的两条切线切点分别为 .
.
 ,求
,求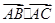 ;
;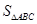 的最大值.
的最大值.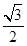 的椭圆
的椭圆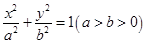 上的点到左焦点
上的点到左焦点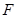 的最长距离为
的最长距离为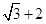 .
.
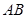 ,若点
,若点 在
在 轴上,且使得
轴上,且使得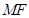 为
为 的一条内角平分线,则称点
的一条内角平分线,则称点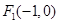 ,
,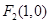 ,圆
,圆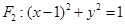 ,一动圆在
,一动圆在 轴右侧与
轴右侧与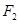 相外切,此动圆的圆心轨迹为曲线C,曲线E是以
相外切,此动圆的圆心轨迹为曲线C,曲线E是以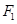 ,
,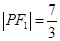 ,求曲线E的标准方程;
,求曲线E的标准方程; 与椭圆E相交于A,B两点,若AB的中点M在曲线C上,求直线
与椭圆E相交于A,B两点,若AB的中点M在曲线C上,求直线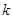 的取值范围。
的取值范围。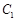 的极坐标方程是
的极坐标方程是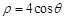 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴正方向建立平面直角坐标系,直线的参数方程是:
轴正方向建立平面直角坐标系,直线的参数方程是: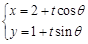 (为参数).
(为参数). ,
,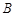 两点,点
两点,点 的直角坐标为
的直角坐标为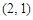 ,若
,若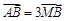 ,求直线的普通方程.
,求直线的普通方程.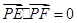 ,由点P向x轴作垂线段PQ,垂足为Q,点M满足
,由点P向x轴作垂线段PQ,垂足为Q,点M满足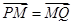 ,点M的轨迹为C.
,点M的轨迹为C. 与曲线C交于A、B两点,点N满足
与曲线C交于A、B两点,点N满足