题目内容
已知两点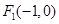 及
及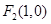 ,点
,点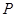 在以
在以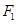 、
、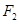 为焦点的椭圆
为焦点的椭圆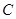 上,且
上,且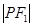 、
、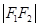 、
、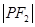 构成等差数列.
构成等差数列.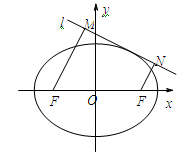
(1)求椭圆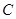 的方程;
的方程;
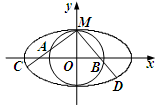
(2)如图,动直线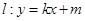 与椭圆
与椭圆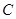 有且仅有一个公共点,点
有且仅有一个公共点,点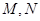 是直线上的两点,且
是直线上的两点,且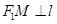 ,
,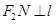 . 求四边形
. 求四边形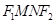 面积
面积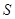 的最大值.
的最大值.
(1)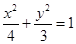 (2)
(2)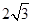
解析试题分析:解:(1)依题意,设椭圆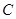 的方程为
的方程为 .
.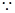
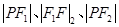 构成等差数列,
构成等差数列,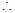
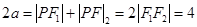 ,
, 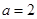 .又
.又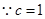 ,
,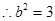 .
. 椭圆
椭圆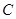 的方程为
的方程为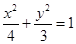 .
. 
(2) 将直线的方程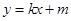 代入椭圆
代入椭圆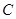 的方程
的方程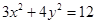 中,得
中,得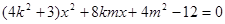 .
.
由直线与椭圆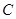 仅有一个公共点知,
仅有一个公共点知,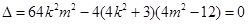 ,
,
化简得: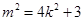 .
.
设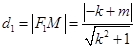 ,
,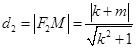 ,
,
(法一)当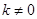 时,设直线的倾斜角为
时,设直线的倾斜角为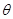 ,
,
则 ,
,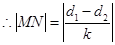 ,
,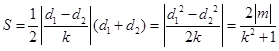
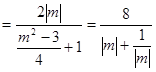 , 11分
, 11分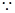
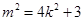 ,
,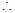 当
当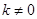 时,
时,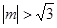 ,
,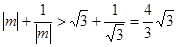 ,
,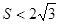 .
.
当 时,四边形
时,四边形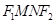 是矩形,
是矩形,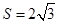 .
.
所以四边形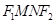 面积
面积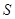 的最大值为
的最大值为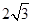 .
.
(法二)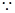
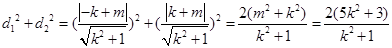 ,
, 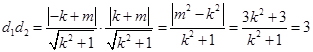 .
. 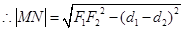
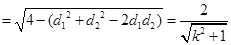 .
.
四边形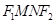 的面积
的面积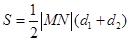
 ,
,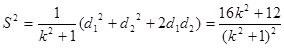
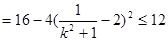 .
.
当且仅当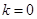 时,
时, ,故
,故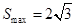 .
.
所以四边形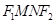 的面积
的面积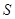 的最大值为
的最大值为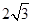 .
.
考点:直线与椭圆的位置关系
点评:主要是考查了直线与椭圆的位置关系的运用,属于中档题。

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 的圆心为
的圆心为 ,动圆
,动圆 过点
过点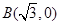 ,且和圆
,且和圆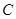 .
.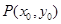 为曲线
为曲线 与曲线
与曲线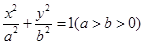 右焦点的直线
右焦点的直线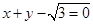 交
交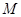 于A,B两点,P为AB的中点,且OP的斜率为
于A,B两点,P为AB的中点,且OP的斜率为 .
.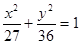 有相同焦点,且经过点
有相同焦点,且经过点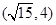 ,求其方程。
,求其方程。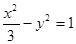 与抛物线
与抛物线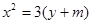 相交于
相交于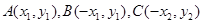
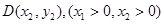 ,直线AC、BD的交点为P(0,p)。
,直线AC、BD的交点为P(0,p)。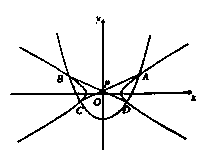
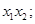
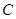 :
: 的焦距为
的焦距为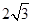 ,离心率为
,离心率为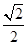 ,其右焦点为
,其右焦点为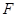 ,过点
,过点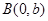 作直线交椭圆于另一点
作直线交椭圆于另一点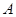 .
.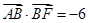 ,求
,求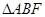 外接圆的方程;
外接圆的方程;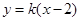 与椭圆
与椭圆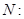
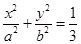 相交于两点
相交于两点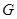 、
、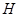 ,且
,且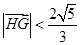 ,求
,求 的取值范围.
的取值范围.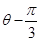 )=1,M,N分别为C与x轴,y轴的交点。
)=1,M,N分别为C与x轴,y轴的交点。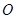 与离心率为
与离心率为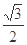 的椭圆
的椭圆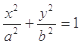 (
(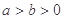 )相切于点
)相切于点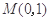 .
.
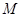 引两条互相垂直的两直线
引两条互相垂直的两直线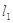 、
、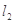 与两曲线分别交于点
与两曲线分别交于点 、
、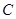 与点
与点 、
、 (均不重合).
(均不重合).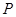 为椭圆上任一点,记点
为椭圆上任一点,记点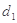 、
、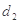 ,求
,求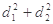 的最大值;
的最大值;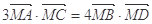 ,求
,求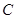 的中心在原点,焦点在
的中心在原点,焦点在 轴上.若椭圆上的点
轴上.若椭圆上的点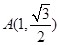 到焦点
到焦点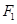 、
、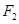 的距离之和等于4.
的距离之和等于4.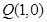 的直线与椭圆交于两点
的直线与椭圆交于两点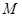 、
、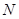 ,当
,当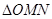 的面积取得最大值时,求直线
的面积取得最大值时,求直线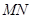 的方程.
的方程.