题目内容
求点A（0，2）到椭圆
+y2=1上的动点的距离的最大值和最小值．
| x2 |
| 4 |
考点：椭圆的参数方程,三角函数的最值
专题：计算题,三角函数的求值,圆锥曲线的定义、性质与方程,坐标系和参数方程
分析：设出椭圆的参数方程，表示出动点B坐标，利用两点间的距离公式表示出距离|AB|，利用二次函数的性质及正弦函数的定义域与值域，即可确定出距离|AB|的最值．
解答：
解：根据椭圆方程，设动点B（2cosθ，sinθ），
∴|AB|2=（2cosθ）2+（sinθ-2）2=4cos2θ+sin2θ-4sinθ+4=-3（sinθ+
）2+
，
当sinθ=-
时，-3（sinθ+
）2+
最大，即|AB|2最大值为
，
则|AB|的最大值为
．
当sinθ=-1，则|AB|2=9，当sinθ=1，则|AB|2=1，则|AB|的最小值为1．
综上，距离的最大值是
，最小值是1．
∴|AB|2=（2cosθ）2+（sinθ-2）2=4cos2θ+sin2θ-4sinθ+4=-3（sinθ+
| 2 |
| 3 |
| 28 |
| 3 |
当sinθ=-
| 2 |
| 3 |
| 2 |
| 3 |
| 28 |
| 3 |
| 28 |
| 3 |
则|AB|的最大值为
2
| ||
| 3 |
当sinθ=-1，则|AB|2=9，当sinθ=1，则|AB|2=1，则|AB|的最小值为1．
综上，距离的最大值是
2
| ||
| 3 |
点评：此题考查了椭圆的参数方程及运用，正弦函数的定义域与值域，二次函数的性质，以及两点间的距离公式，熟练掌握公式是解本题的关键．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
相关题目
下列四个集合：
①A={x|y=x2+1}；
②B={y|y=x2+1，x∈R}；
③C={（x，y）|y=x2+1，x∈R}；
④D={不小于1的实数}．
其中相同的集合是（ ）
①A={x|y=x2+1}；
②B={y|y=x2+1，x∈R}；
③C={（x，y）|y=x2+1，x∈R}；
④D={不小于1的实数}．
其中相同的集合是（ ）
| A、①与② | B、①与④ |
| C、②与③ | D、②与④ |
已知a是实数，
是纯虚数，则a等于（ ）
| a+i |
| 1-i |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
若a、b、c是从集合{1，2，3，4，5}中任意选取的3个不重复的数，则ab+c为奇数的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
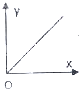
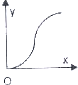
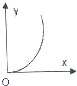
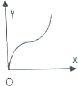
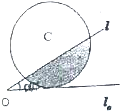如图，已知直线l和圆C，当l从l0开始在平面上绕点O按逆时针方向匀速转动（转动角度不超过90°）时，它扫过的圆内阴影部分的面积y是时间x的函数，这个函数的图象大致是（ ）
