题目内容

若直线2ax-by+2=0（a＞0，b＞0）经过圆x2+y2+2x-4y+1=0的圆心，则
1
a
+
1
b
的最小值是
 
．
考点：基本不等式在最值问题中的应用,直线与圆的位置关系
专题：不等式的解法及应用,直线与圆
分析：求出圆的圆心坐标，代入直线方程，得到ab关系式，然后通过”1“的代换利用基本不等式求解即可．
解答： 解：x2+y2+2x-4y+1=0的圆心（-1，2），
所以直线2ax-by+2=0（a＞0，b＞0）经过圆心，可得：a+b=1，
1
a
+
1
b
=（
1
a
+
1
b
）（a+b）=2+
b
a
+
a
b
≥2+
2
，当且仅当a=b=
1
2
．
1
a
+
1
b
的最小值是：2+
2
．
故答案为：2+
2
．
点评：本题考查直线与圆的位置关系的应用，基本不等式求解函数的最值，考查转化思想以及计算能力．
练习册系列答案
相关题目
求下列函数的导数
（1）y=log2x                 （2）y=2ex
（3）y=2x3-3x2-4             （4）y=3cosx-4sinx
（5）y=cos
x
3
                   （6）y=
x-1
．
已知f（x）=x3+x2-x，求f（x）的导数．
已知f（x）=ax-lnx，x∈（0，e]，a∈R．
（1）若a=1，求f（x）的极小值；
（2）是否存在实数a，使f（x）的最小值为3．
设（1+x）n=a0+a1x+…+anxn，若展开式中系数最大的项的系数是70，则a1+a2+‥‥+an=
 
．
已知α、β均为锐角，且cosα=
1
5
，cos（α+β）=
2
-4
3
10
，求角β．
已知cos（π-α）=
2
3
2
，α∈（-π，0）．求cos2（
π
4
-
α
2
）+sin（3π+
α
2
）+sin（
3
2
π-
α
2
）
已知非零向量
a
，
b
夹角为θ，若
a
+
b
=（3，-6），
a
-
b
=（3，-2），则cosθ=
 
．
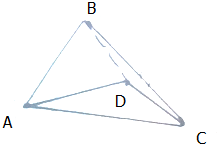如图，在四面体ABCD中，△ABD是正三角形，AB⊥BC，AD⊥DC，AC=2AB，则直线DC与平面ABD所成角的正弦值等于
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网