题目内容
设函数f(x)=sin2ωx+2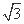 sin ωx·cos ωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
sin ωx·cos ωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(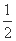 ,1).
,1).
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点( ,0),求函数f(x)的值域.
,0),求函数f(x)的值域.
解:(1)f(x)=sin2ωx-cos2ωsin x+2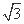 sin ωx·cos ωx+λ
sin ωx·cos ωx+λ
=-cos 2ωx+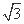 sin 2ωx+λ
sin 2ωx+λ
=2sin(2ωx-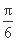 )+λ.
)+λ.
由直线x=π是y=f(x)图象的一条对称轴,
可得sin(2ωπ-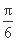 )=±1,
)=±1,
所以2ωπ-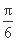 =kπ+
=kπ+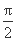 (k∈Z),
(k∈Z),
即ω= +
+ (k∈Z).
(k∈Z).
又ω∈(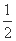 ,1),k∈Z,
,1),k∈Z,
所以k=1,故ω= .
.
所以f(x)的最小正周期是 .
.
(2)由y=f(x)的图象过点( ,0),
,0),
得f( )=0,
)=0,
即λ=-2sin( ×
×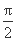 -
-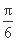 )
)
=-2sin =-
=- ,
,
即λ=- .
.
故f(x)=2sin( x-
x-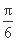 )-
)- .
.
所以函数f(x)的值域为[-2- ,2-
,2- ].
].

练习册系列答案
相关题目
 +
+ 的最小值是( )
的最小值是( )
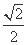 ,求α的值.
,求α的值.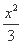 -
-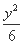 =1 (B)
=1 (B) 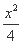 -
-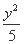 =1
=1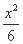 -
-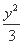 =1 (D)
=1 (D)  -
-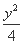 =1
=1 +
+ =1(a>b>0)的两个焦点,P为椭圆C上一点,且
=1(a>b>0)的两个焦点,P为椭圆C上一点,且 ⊥
⊥ ,若△PF1F2的面积为9,则b= .
,若△PF1F2的面积为9,则b= .