题目内容
2．不等式kx2+kx+1＞0恒成立的充要条件是0≤k＜4．分析 根据题意，将原问题转化为函数f（x）=kx2+kx+1＞0恒成立；分两种情况讨论：①、k=0时，易得f（x）=1＞0，符合题意；②、k≠0时，若f（x）=kx2+kx+1＞0恒成立，必有k＞0且k2-4k＜0，解可得k的范围；综合2种情况即可得答案．
解答 解：根据题意，不等式kx2+kx+1＞0可以转化为函数f（x）=kx2+kx+1＞0恒成立；
①、k=0时，f（x）=1＞0，符合题意；
②、k≠0时，若f（x）=kx2+kx+1＞0恒成立，
必有k＞0且k2-4k＜0，
解可得0＜k＜4；
综合可得k的取值范围是0≤k＜4；
故答案为：0≤k＜4．
点评 本题考查不等式的恒成立问题，注意分析k=0时的情况．
练习册系列答案
相关题目
12．现代产品的销售离不开广告的促销活动，某公司代理一种国际品牌智能环境检测设备，其广告费用x（单位：万元）与年销售量t（单位：件）的统计数据如表所示：
这里所给出的数据表示t对x呈线性回归关系$\stackrel{∧}{t}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$．
[参考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$]．
（1）根据所给数据求出线性回归方程；
（2）将（1）中的$\stackrel{∧}{t}$近似地看作产品的实际年销售量t，若该产品的销售单价g（x）（单位：万元）与广告费x的近似关系是g（x）=$\left\{\begin{array}{l}{17-2x（x∈{N}^{*}，且1≤x≤5）}\\{6-\frac{2}{x}（x∈{N}^{*}，且6≤x≤10）}\end{array}\right.$试问当公司投入广告费用多少万元时，公司每年获得的销售收入最大，最大销售收入是多少万元？
| 广告费用x（万元） | 3 | 4 | 5 | 6 |
| 年销售量t（件） | 25 | 30 | 40 | 45 |
[参考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$]．
（1）根据所给数据求出线性回归方程；
（2）将（1）中的$\stackrel{∧}{t}$近似地看作产品的实际年销售量t，若该产品的销售单价g（x）（单位：万元）与广告费x的近似关系是g（x）=$\left\{\begin{array}{l}{17-2x（x∈{N}^{*}，且1≤x≤5）}\\{6-\frac{2}{x}（x∈{N}^{*}，且6≤x≤10）}\end{array}\right.$试问当公司投入广告费用多少万元时，公司每年获得的销售收入最大，最大销售收入是多少万元？
14．
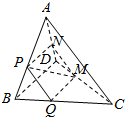如图，在四面体ABCD中，截面PQMN是正方形，且PQ∥AC，则下列命题中，错误的是（ ）
如图，在四面体ABCD中，截面PQMN是正方形，且PQ∥AC，则下列命题中，错误的是（ ）| A． | AC⊥BD | B． | AC∥截面PQMN | ||
| C． | AC=BD | D． | 异面直线PM与BD所成的角为45° |
11．两线段AB、CD不在同一平面内，如果AC=BD，AD=BC，则AB与CD（ ）
| A． | 垂直 | B． | 平行 | C． | 相交 | D． | 以上都不对 |
9．在△ABC中，a+b+10c=2（sinA+sinB+10sinC），A=60°，则a=（ ）
| A． | 4 | B． | $\sqrt{3}$ | C． | $2\sqrt{3}$ | D． | 不确定 |