题目内容
7．方程x=2-$\sqrt{-{y}^{2}+2y+3}$表示的曲线与直线x=2围成的图形面积是π．分析 x=2-$\sqrt{-{y}^{2}+2y+3}$ 可以化简成：（x-2）2+（y-1）2=2 （x≤2），它表示的曲线是个半径为$\sqrt{2}$的半圆，即可得出结论．
解答 解：x=2-$\sqrt{-{y}^{2}+2y+3}$ 可以化简成：（x-2）2+（y-1）2=2 （x≤2）
它表示的曲线是个半径为$\sqrt{2}$的半圆
与x=2围成的图形就是个半圆，面积是$\frac{1}{2}•π•2$=π．
故答案为：π．
点评 本题考查圆的方程，考查学生的计算能力，比较基础．
练习册系列答案
名校课堂系列答案
相关题目
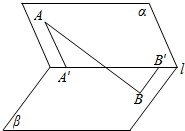如图，二面角a-l-β为60°，A∈a，B∈β，AA′⊥l交l于A′，BB′⊥l交1于B′，若AA′=2，BB′=1，A′B′=$\sqrt{3}$．