Question

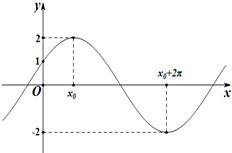已知函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，-

π

2

＜φ＜0）的图象与y轴的交点为（0，1），它在y轴右侧的第一个最高点和第一个最低点的坐标分别为（x₀，2）和（x₀+2π，-2）．
（1）求函数f（x）的解析式；
（2）若锐角θ满足f（2θ+

2π

3

）=

2

3

，求f（2θ）的值．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：

分析：（1）由题意可得A=2，由周期公式可得ω=

1

2

，再由f（0）=1可得φ=-

π

3

，可得f（x）=2cos（

1

2

x-

π

3

）；
（2）由已知可得cosθ=

1

3

，进而可得sinθ=

2 2

3

，而f（2θ）=2（

1

2

cosθ+

3

2

sinθ），代值计算可得．

解答： 解：（1）由题意可得A=2，

T

2

=

π

ω

=2π，解得ω=

1

2

，
∴f（x）=2cos（

1

2

x+φ），
由图象可知f（0）=2cosφ=1，∴cosφ=

1

2

，
又-

π

2

＜φ＜0，∴φ=-

π

3

∴f（x）=2cos（

1

2

x-

π

3

）
（2）∵f(2θ+

2π

3

)=

2

3

，∴2cosθ=

2

3

，
∴cosθ=

1

3

，∵θ为锐角，∵sinθ=

2 2

3

∴f（2θ）=2cos（θ-

π

3

）=2（

1

2

cosθ+

3

2

sinθ）
=2（

1

2

×

1

3

+

3

2

×

2 2

3

）=

1+2 6

3

，
即f（2θ）的值为

1+2 6

3

点评：本题考查三角函数的图象与解析式，涉及三角函数和差角的公式，属基础题．