题目内容
已知Q为椭圆x2+2y2=98上一动点,P(0,5)为一定点,求点P到椭圆的最大和最小距离以及此时Q的坐标.
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析:可设出Q(7
cosα,7sinα),(0≤α<2π),求出|PQ|,化简整理成关于sinα的式子,并配方,再由正弦函数的值域,结合二次函数的顶点,即可得到最值.
| 2 |
解答:
解:由于Q为椭圆x2+2y2=98上一动点,
可设Q(7
cosα,7sinα),(0≤α<2π),
则|PQ|=
=
=
=
由于sinα∈[-1,1],
则当sinα=-
∈[-1,1],此时cosα=±
,即M(4
,-5)或(-4
,-5)时,
|PQ|取最大值,且为2
;
当sinα=1时,cosα=0,即有M(0,7),|PQ|取最小值,且为2.
可设Q(7
| 2 |
则|PQ|=
(0-7
|
=
| 98cos2α+49sin2α-70sinα+25 |
=
| 123-49sin2α-70sinα |
=
148-49(sinα+
|
由于sinα∈[-1,1],
则当sinα=-
| 5 |
| 7 |
2
| ||
| 7 |
| 3 |
| 3 |
|PQ|取最大值,且为2
| 37 |
当sinα=1时,cosα=0,即有M(0,7),|PQ|取最小值,且为2.
点评:本题考查椭圆方程,主要是运用参数方程解题,考查三角函数的化简和正弦函数的值域,考查运算能力,属于中档题.

练习册系列答案
相关题目
已知向量
=(1,n),
=(-1,n),若2
+
与
垂直,则|
|=( )
| a |
| b |
| a |
| b |
| b |
| a |
| A、1 | ||||
B、
| ||||
C、
| ||||
| D、4 |
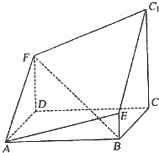 如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1
如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1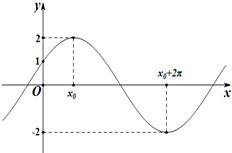 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,-
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,-