题目内容
若
是函数f(x)=sin2x+acos2x(a∈R且为常数)的零点,则f(x)的最大值是 _
| π |
| 4 |
考点:三角函数中的恒等变换应用,函数零点的判定定理
专题:计算题
分析:由f(
)=sin
+acos2
=0,可求得a=-2,于是f(x)=sin2x-2cos2x转化为:f(x)=
sin(2x-
)-1,从而可求f(x)的最大值.
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
解答:
解:∵
是函数f(x)=sin2x+acos2x(a∈R,为常数)的零点,
∴f(
)=sin
+acos2
=0,
∴1+
a=0,
∴a=-2.
∴f(x)=sin2x-2cos2x
=sin2x-cos2x-1
=
sin(2x-
)-1,
∴f(x)的最大值为
-1.
故答案为:
-1.
| π |
| 4 |
∴f(
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
∴1+
| 1 |
| 2 |
∴a=-2.
∴f(x)=sin2x-2cos2x
=sin2x-cos2x-1
=
| 2 |
| π |
| 4 |
∴f(x)的最大值为
| 2 |
故答案为:
| 2 |
点评:本题考查函数的零点,由f(
)=0求得a的值是基础,利用辅助角公式转化是关键,属于中档题.
| π |
| 4 |

练习册系列答案
相关题目
方程x2+3(y-1)2=9的曲线关于( )对称.
| A、x轴 | B、y轴 |
| C、原点 | D、以上都不对 |
已知函数f(x)=x2+2ax+2在[-5,5]上单调,则实数a的取值范围是( )
| A、(-∞,-5] |
| B、[5,+∞) |
| C、[-5,5] |
| D、(-∞,-5]∪[5,+∞) |
现有四个函数:①y=x•sinx;②y=x•cosx;③y=x•|cosx|;④y=x•2x的图象(部分)如下:
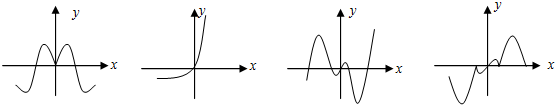
则按照从左到右图象对应的函数序号安排正确的一组是( )
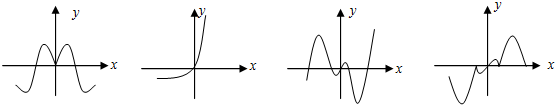
则按照从左到右图象对应的函数序号安排正确的一组是( )
| A、①④③② | B、③④②① |
| C、④①②③ | D、①④②③ |
已知f(x)是R上的奇函数,且f(x+4)=f(x),当x∈(0,2)时,f(x)=x2,则f(7)的值为( )
| A、-1 | B、4 | C、1 | D、0 |
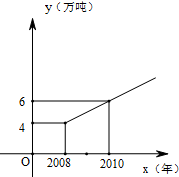 某市实施“限塑令”后,2008年大约减少塑料消耗约4万吨.调查结果分析显示,从2008年开始,五年内该市因实施“限塑令”而减少的塑料消耗量y(万吨)随着时间x(年)逐年成直线上升,y与x之间的关系如图所示.
某市实施“限塑令”后,2008年大约减少塑料消耗约4万吨.调查结果分析显示,从2008年开始,五年内该市因实施“限塑令”而减少的塑料消耗量y(万吨)随着时间x(年)逐年成直线上升,y与x之间的关系如图所示.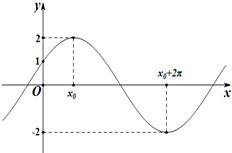 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,-
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,-