题目内容
在等差数列{an}中,a1=2,a3+a5=10,则a7=( )
| A、5 | B、8 | C、10 | D、14 |
考点:等差数列的性质,等差数列的通项公式
专题:等差数列与等比数列
分析:由等差数列{an}中,a1=2,且有a3+a5=10,利用等差数列的通项公式先求出公差d,再求a7.
解答:
解:∵等差数列{an}中,a1=2,a3+a5=10,
∴a1+a7=a3+a5=10,
∴a7=10-a1=8.
故选:B.
∴a1+a7=a3+a5=10,
∴a7=10-a1=8.
故选:B.
点评:本题考查等差数列的性质和应用,解题时要认真审题,仔细解答,注意等差数列通项公式的合理运用.

练习册系列答案
相关题目
如果若干个函数的图象经过平移后能够重合,则称这些函数为“同簇函数”.给出下列函数:
①f(x)=sinxcosx,
②f(x)=
sin2x+2,
③f(x)=2sin(x+
),
④f(x)=sinx-
cosx,
其中属于“同簇函数”的是( )
①f(x)=sinxcosx,
②f(x)=
| 2 |
③f(x)=2sin(x+
| π |
| 4 |
④f(x)=sinx-
| 3 |
其中属于“同簇函数”的是( )
| A、①② | B、①④ | C、②③ | D、③④ |
设四边形ABCD的两条对角线为AC,BD,则“四边形ABCD为菱形”是“AC⊥BD”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
在如图所示的空间直角坐标系O-xyz中,一个四面体的顶点坐标分别为(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出的编号为①,②,③,④的四个图,则该四面体的正视图和俯视图分别为( )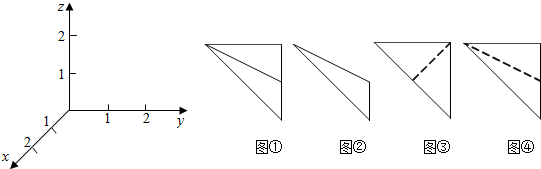

| A、①和② | B、③和① |
| C、④和③ | D、④和② |
若二项式(2x+
)7的展开式中
的系数是84,则实数a=( )
| a |
| x |
| 1 |
| x3 |
| A、2 | ||||
B、
| ||||
| C、1 | ||||
D、
|
已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-3x,则函数g(x)=f(x)-x+3的零点的集合为( )
| A、{1,3} | ||
| B、{-3,-1,1,3} | ||
C、{2-
| ||
D、{-2-
|
