题目内容

已知双曲线
x2
a2
-y2=1的一个顶点与抛物线y2=4x的焦点重合，则该双曲线的离心率为
 
．
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由题意可求得a=1，b=1，c=
2
，从而写出离心率即可．
解答： 解：∵抛物线y2=4x的焦点（1，0），
∴a=1，
又∵b=1，∴c=
2
，
∴e=
c
a
=
2
；
故答案为：
2
．
点评：本题考查了圆锥曲线的性质，属于基础题．
练习册系列答案
相关题目
“x＜0”是“ln（x+1）＜0”的（　　）条件．
A、充分不必要
B、必要不充分
C、充分必要
D、既不充分也不必要
若{1，2}⊆A⊆{1，2，3，4，5 }，则集合A的个数是
 
．
三棱锥A-BCD中，若AB⊥CD，AD⊥BC，则异面直线AC和BD所成的角为
 
．
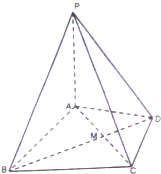如图，在四棱锥P-ABCD中，PA⊥面ABCD，△ABC是正三角形，AC△与BD的交点M恰好是AC的中点，又是PA=AB=2，∠CDA=120°．
（Ⅰ）求证：BD⊥PC；
（Ⅱ）求二面角A-PC-D的余弦值．
已知
i
，
j
，
k
是两两垂直的单位向量，
a
=2
i
-
j
+
k
，
b
=
i
+
j
-3
k
，则
a
•
b
=
 
．
（1）（2
4
5
）0+2-2×（2
1
4
）- 
1
2
-（0.01） 
1
2
；
（2）2（lg
2
）2+lg
2
•lg5+
(lg
2
)2-lg2+1
．
下面四个命题：
①分别在两个平面内的直线平行
②若两个平面平行，则其中一个平面内的任何一条直线必平行于另一个平面
③如果一个平面内的两条直线平行于另一个平面，则这两个平面平行
④如果一个平面内的任何一条直线平行于另一个平面，则这两个平面平行
其中正确的命题是（　　）
A、①②B、②④C、①③D、②③
已知定点A、B，且|AB|=6，动点P满足|PA|-|PB|=4，则PA的最小值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网