题目内容
17.若x2+bx+c<0的解集为(2,3),解关于x的不等式:x2+abx+ca2>0(a∈R)分析 由于x2+bx+c<0的解集为(2,3),利用根与系数的关系求出b,c的值.x2+abx+ca2>0化为x2-5ax+6a2>0即为(x-2a)(x-3a)>0,分类讨论解得即可.
解答 解:∵不等式x2+bx+c<0的解集为(2,3),
∴2,3是一元二次方程x2+bx+c=0的两个实数根,
∴2+3=5=-b,2×3=6=c.
∴b=-5,c=6,
∴x2+abx+ca2>0化为x2-5ax+6a2>0即为(x-2a)(x-3a)>0
当a>0时,2a<3a,解得x<2a或x>3a,故不等式的解集为{x|x<2a或x>3a},
当a=0时,解得x≠0,故不等式的解集为{x|x≠0}.
当a<0时,2a>3a,解得x<3a或x>2a,故不等式的解集为{x|x<3a或x>2a}.
点评 本题考查了一元二次不等式的解法、一元二次方程的根与系数的关系,考查了推理能力和计算能力,属于中档题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
5.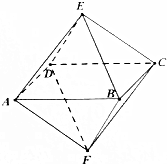 如图,已知一个八面体的各条棱长均为1,四边形ABCD为正方形,给出下列命题:
如图,已知一个八面体的各条棱长均为1,四边形ABCD为正方形,给出下列命题:
①不平行的两条棱所在的直线所成的角是60°或90°;
②四边形AECF是正方形;
③点A到平面BCE的距离为1.
其中正确的命题有( )
 如图,已知一个八面体的各条棱长均为1,四边形ABCD为正方形,给出下列命题:
如图,已知一个八面体的各条棱长均为1,四边形ABCD为正方形,给出下列命题:①不平行的两条棱所在的直线所成的角是60°或90°;
②四边形AECF是正方形;
③点A到平面BCE的距离为1.
其中正确的命题有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
12.空间四边形(四条边不在同一平面的四边形)中异面直线的对数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
9.已知点O是△ABC的外心,a、b、c分别为角A、B、C的对边,2c2-c+b2=0,则$\overrightarrow{BC}$•$\overrightarrow{AO}$的取值范围是( )
| A. | [-$\frac{1}{4}$,2) | B. | (-$\frac{1}{8}$,0) | C. | (-$\frac{1}{8}$,$\frac{1}{24}$] | D. | (0,$\frac{1}{3}$) |
16.执行如图所示的程序框图,输出的结果是( )


| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
 甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取6次.得到甲、乙两位学生成绩的茎叶图.
甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取6次.得到甲、乙两位学生成绩的茎叶图. 如图,平面上有一组间距为5的平行线(无数条),把一根长为2的针投到平面上,我们可以通过下面的方法计算这根针与其中一条直线相交的概率:设针的中点到距其最近的一条直线的距离为d,针所在的倾斜角为θ,则d≤sinθ时,针与该直线有公共点.根据这种方法,计算出相应的概率为$\frac{4}{5π}$.
如图,平面上有一组间距为5的平行线(无数条),把一根长为2的针投到平面上,我们可以通过下面的方法计算这根针与其中一条直线相交的概率:设针的中点到距其最近的一条直线的距离为d,针所在的倾斜角为θ,则d≤sinθ时,针与该直线有公共点.根据这种方法,计算出相应的概率为$\frac{4}{5π}$.