题目内容
9.已知点O是△ABC的外心,a、b、c分别为角A、B、C的对边,2c2-c+b2=0,则$\overrightarrow{BC}$•$\overrightarrow{AO}$的取值范围是( )| A. | [-$\frac{1}{4}$,2) | B. | (-$\frac{1}{8}$,0) | C. | (-$\frac{1}{8}$,$\frac{1}{24}$] | D. | (0,$\frac{1}{3}$) |
分析 由b2=c-2c2>0得出c的范围,用$\overrightarrow{AB}$表示出$\overrightarrow{BC}$,根据向量的数量积定义得出$\overrightarrow{BC}•\overrightarrow{AO}$ 关于c的函数,由此求出此函数的值域.
解答 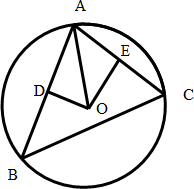 解:如图所示:过O作OD⊥AB于D,OE⊥AC于E,则D,E分别是AB,AC的中点.
解:如图所示:过O作OD⊥AB于D,OE⊥AC于E,则D,E分别是AB,AC的中点.
∴$\overrightarrow{BC}•AO$=($\overrightarrow{AC}$-$\overrightarrow{AB}$)•$\overrightarrow{AO}$=$\overrightarrow{AC}•\overrightarrow{AO}$-$\overrightarrow{AB}•\overrightarrow{AO}$=AC•AE-AB•AD=$\frac{{b}^{2}{-c}^{2}}{2}$,
∵2c2-c+b2=0,∴b2=c-2c2>0,解得0<c<$\frac{1}{2}$,
∴$\overrightarrow{BC}•\overrightarrow{AO}$=$\frac{c-{3c}^{2}}{2}$=-$\frac{3}{2}$${(c-\frac{1}{6})}^{2}$+$\frac{1}{24}$,故当c=$\frac{1}{6}$时,$\overrightarrow{BC}•\overrightarrow{AO}$ 取得最大值为$\frac{1}{24}$;
当c趋于$\frac{1}{2}$时,$\overrightarrow{BC}•\overrightarrow{AO}$ 趋于最小值为-$\frac{1}{8}$,则$\overrightarrow{BC}$•$\overrightarrow{AO}$的取值范围是(-$\frac{1}{8}$,$\frac{1}{24}$],
故选:C.
点评 本题考查了平面向量的数量级运算,二次函数的最值,属于中档题.

| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$或$\frac{2π}{3}$ |
| A. | {2,4} | B. | {-3,-1} | C. | {-3,-1,0} | D. | {0,2,4} |
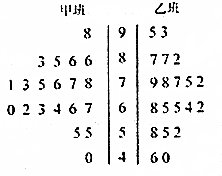 甲、乙两班各20个学生某次数学考试成绩(单位:分)的茎叶图如图所示,根据茎叶图解决下列问题.
甲、乙两班各20个学生某次数学考试成绩(单位:分)的茎叶图如图所示,根据茎叶图解决下列问题.