题目内容
1.一个三角形的直观图是腰长为$\sqrt{6}$,底为4的等腰三角形,则原三角形面积是8.分析 斜二测画法中,原图形的面积与直观图的面积之比为2$\sqrt{2}$,即可求出原图形的面积.
解答 解:一个三角形的直观图是腰长为$\sqrt{6}$,底为4的等腰三角形,面积为$\frac{1}{2}×4×\sqrt{6-4}$=2$\sqrt{2}$
由斜二测画法可得.原图形的面积与直观图的面积之比为2$\sqrt{2}$,原三角形的面积为8.
故答案为:8.
点评 本题考查平面图形的直观图,考查计算能力,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下列说法正确的是( )
| A. | 都与直线a相交的两条直线确定一个平面 | |
| B. | 两条直线确定一个平面 | |
| C. | 过一条直线的平面有无数多个 | |
| D. | 两个相交平面的交线是一条线段 |
9.定义n!=1×2×…×n,下面是求10!的程序,则_____处应填的条件是( )


| A. | i>10 | B. | i>11 | C. | i<=10 | D. | i<=11 |
13.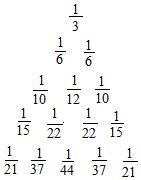 如图所示的数阵中,用A(m,n)表示第m行的第n个数,则依次规律A(8,2)为( )
如图所示的数阵中,用A(m,n)表示第m行的第n个数,则依次规律A(8,2)为( )
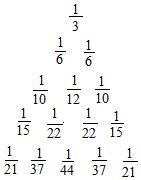 如图所示的数阵中,用A(m,n)表示第m行的第n个数,则依次规律A(8,2)为( )
如图所示的数阵中,用A(m,n)表示第m行的第n个数,则依次规律A(8,2)为( )| A. | $\frac{1}{45}$ | B. | $\frac{1}{86}$ | C. | $\frac{1}{122}$ | D. | $\frac{1}{167}$ |
11.已知函数f(x)是定义在R上的可导函数,其导函数为f′(x),则命题P:“?x1,x2∈R,且x1≠x2,|$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$|<2017”是命题Q:“?x∈R,|f′(x)|<2017”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |