题目内容
9.在平面直角坐标系xOy中,若双曲线$\frac{{y}^{2}}{{m}^{2}+1}$-$\frac{{x}^{2}}{2m+6}$=1的离心率为$\sqrt{5}$,则实数m的值为1或-$\frac{1}{2}$.分析 根据双曲线的方程求出a,b的值,结合双曲线的离心率建立方程关系进行求解即可.
解答 解:∵m2+1≥1,
∴由双曲线$\frac{{y}^{2}}{{m}^{2}+1}$-$\frac{{x}^{2}}{2m+6}$=1的方程得a2=m2+1,b2=2m+6>0,得m>-3,
则c2=m2+1+2m+6=m2+2m+7,
∵双曲线的离心率e=$\sqrt{5}$,
∴e2=$\frac{{c}^{2}}{{a}^{2}}$=$\frac{{m}^{2}+2m+7}{{m}^{2}+1}$=5,
即m2+2m+7=5m2+5,
即4m2-2m-2=0,得2m2-m-1=0,
得m=1或m=-$\frac{1}{2}$,
故答案为:1或-$\frac{1}{2}$,
点评 本题主要考查双曲线离心率的应用,根据条件建立方程关系是解决本题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
20.《九章算术》是我国古代内容极为丰富的数学名著,卷一《方田》[三三]:“今有宛田,下周三十步,径十六步.问为田几何?”译成现代汉语其意思为:有一块扇形的田,弧长30步,其所在圆的直径是16步,问这块田的面积是多少(平方步)?( )
| A. | 120 | B. | 240 | C. | 360 | D. | 480 |
18.双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{4}$=1的左右焦点分别为F1、F2,点P为双曲线上任意一点,点Q是以点P为圆心,|PF1|为半径的圆上的任意点,那么|QF2|( )
| A. | 有最小值8 | B. | 有最大值8 | C. | 有最小值4$\sqrt{5}$ | D. | 有最大值4$\sqrt{5}$ |
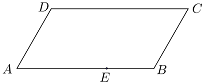 图为一块平行四边形园地ABCD,经测量,AB=20米,BC=10米,∠ABC=120°,拟过线段AB上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),将该园地分为面积之比为3:1的左、右两部分分别种植不同的花卉,设EB=x,EF=y(单位:米)
图为一块平行四边形园地ABCD,经测量,AB=20米,BC=10米,∠ABC=120°,拟过线段AB上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),将该园地分为面积之比为3:1的左、右两部分分别种植不同的花卉,设EB=x,EF=y(单位:米)