题目内容
14.若函数y=f(x)的图象与函数y=3x+a的图象关于直线y=-x对称,且f(-1)+f(-3)=3,则实数a等于( )| A. | -1 | B. | 1 | C. | 2 | D. | 4 |
分析 设(x,y)为函数y=f(x)的图象上的一点,则关于直线y=-x对称的点为(-y,-x).代入函数y=3x+a可得:f(x)=a-log3(-x).即可得出.
解答 解:设(x,y)为函数y=f(x)的图象上的一点,则关于直线y=-x对称的点为(-y,-x).
代入函数y=3x+a可得:-x=3-y+a,∴-y+a=log3(-x),即f(x)=a-log3(-x).
∵f(-1)+f(-3)=3,∴a-0+a-log33=3,解得a=2.
故选:C.
点评 本题考查了反函数的性质、方程的解法、轴对称的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.某校共有学生2000名,各年级男、女生人数如表中所示.已知在全校学生中随机抽取1名,抽到二年级女生的概率是0.18.现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为( )
| 一年级 | 二年级 | 三年级 | |
| 女生 | 363 | x | y |
| 男生 | 387 | 390 | z |
| A. | 12 | B. | 16 | C. | 18 | D. | 24 |
6.若集合P={x|4<x<10},Q={x|3<x<7},则P∪Q等于( )
| A. | {x|3<x<7} | B. | {x|3<x<10} | C. | {x|3<x<4} | D. | {x|4<x<7} |
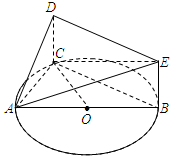 如图,AB是△ABC外接圆O的直径,四边形DCBE为矩形,且DC⊥平面ABC,AB=4,BE=1.
如图,AB是△ABC外接圆O的直径,四边形DCBE为矩形,且DC⊥平面ABC,AB=4,BE=1.