题目内容
2．函数f（x）=1+sin2x得最小正周期是π．分析 利用二倍角公式化简函数的解析式，再利用余弦函数的周期性求得函数的最小正周期．
解答 解：函数f（x）=1+sin2x=1+$\frac{1-cos2x}{2}$=$\frac{3}{2}$-$\frac{1}{2}$cos2x的最小正周期为$\frac{2π}{2}$=π，
故答案为：π．
点评 本题主要考查二倍角公式的应用，余弦函数的周期性，属于基础题．
练习册系列答案
相关题目
17．已知双曲线${x^2}-\frac{y^2}{m}=1$与抛物线y2=8x的一个交点为P，F为抛物线的交点，若|PF|=5，则双曲线的离心率为（ ）
| A． | $\sqrt{2}$ | B． | 4 | C． | $\sqrt{3}$ | D． | 2 |
7．已知数列{an}满足：an=$\left\{\begin{array}{l}{1，1≤n≤2016}\\{2•（\frac{1}{3}）^{n-2016}，n≥2017}\end{array}\right.$，设Sn表示数列{an}的前n项和．则下列结论正确的是（ ）
| A． | $\lim_{n→∞}{a_n}$和$\lim_{n→∞}{S_n}$都存在 | B． | $\lim_{n→∞}{a_n}$和$\lim_{n→∞}{S_n}$都不存在 | ||
| C． | $\lim_{n→∞}{a_n}$存在，$\lim_{n→∞}{S_n}$不存在 | D． | $\lim_{n→∞}{a_n}$不存在，$\lim_{n→∞}{S_n}$存在 |
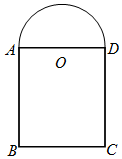设计人员要用10米长的材料（材料的宽度不计）建造一个窗子的边框，如图所示，窗子是由一个矩形ABCD和以AD为直径的半圆组成，窗子的边框不包括矩形的AD边，设半圆的半径为OA=r（米），窗子的透光面积为S（平方米）．