题目内容
12．已知x，y满足$\left\{\begin{array}{l}x-y+2≥0\\ x+y≤2\\ x≤3\end{array}\right.$，则z=2x+y的最大值为5．分析 作出题中不等式组表示的平面区域，得如图的△ABC及其内部，再将目标函数z=2x+y对应的直线进行平移，然后求z=2x+y的最大值．
解答 
解：作出不等式组$\left\{\begin{array}{l}x-y+2≥0\\ x+y≤2\\ x≤3\end{array}\right.$表示的平面区域，
设z=F（x，y）=2x+y，将直线l：z=2x+y进行平移，
当l经过点A时，目标函数z达到最大值，由$\left\{\begin{array}{l}{x=3}\\{x+y=2}\end{array}\right.$解得A（3，-1）
∴z最大值=F（3，-1）=2×3-1=5．
故答案为：5．
点评 本题给出二元一次不等式组，求目标函数z=2x+y的最大值，着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识，属于基础题．
练习册系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
6．设复数z1，z2在复平面内的对应点关于虚轴对称，z1=1+2i，i为虚数单位，则z1z2=（ ）
| A． | 1-2i | B． | -5 | C． | 5 | D． | 5i |
20．已知一种腌菜食品按行业生产标准分为A，B，C三个等级，现针对某加工厂同一批次的三个等级420箱腌菜进行质量检测，采用分层抽样的方法进行抽取．设从三个等级A，B，C中抽取的箱数分别为m，n，t，若2t=m+n，则420箱腌菜中等级为C级的箱数为（ ）
| A． | 110 | B． | 120 | C． | 130 | D． | 140 |
4．
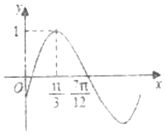函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，$|φ|＜\frac{π}{2}$）的图象如图所示，为了得到g（x）=Asinωx的图象，可以将f（x）的图象（ ）
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，$|φ|＜\frac{π}{2}$）的图象如图所示，为了得到g（x）=Asinωx的图象，可以将f（x）的图象（ ）| A． | 向左平移$\frac{π}{12}$个单位长度 | B． | 向右平移$\frac{π}{12}$个单位长度 | ||
| C． | 向左平移$\frac{π}{6}$个单位长度 | D． | 向右平移$\frac{π}{6}$个单位长度 |