Question

12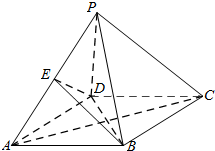．如图，四棱锥P-ABCD中，底面ABCD是边长为 4的菱形，PD=PB=4，∠BAD=60°，E为PA中点．
（Ⅰ）求证：PC∥平面EBD；
（Ⅱ）求证：平面EBD⊥平面PAC；
（Ⅲ）若PA=PC，求三棱锥C-ABE的体积．

Answer 1

分析 （Ⅰ）设AC∩BD=O，连结EO，证明EO∥PC．即可证明PC∥平面EBD．
（Ⅱ）连结PO，证明PO⊥BD．AC⊥BD．即可证明BD⊥平面PAC．然后说明平面EBD⊥平面PAC．
（Ⅲ）利用V_C-ABE=V_E-ABC，求解即可．

解答 （本小题14分）
解（Ⅰ）设AC∩BD=O，连结EO，
∵E为PA中点，O为AC中点，
∴EO∥PC．
又∵EO?平面EBD，PC?平面EBD，
∴PC∥平面EBD．        …（5分）
（Ⅱ）连结PO，
∵PD=PB，O为BD中点，
∴PO⊥BD．
又∵底面ABCD为菱形，
∴AC⊥BD．
∵PO∩AC=O，
∴BD⊥平面PAC．
又∵BD?平面EBD，
∴平面EBD⊥平面PAC．…（10分）
（Ⅲ）V_C-ABE=V_E-ABC…（12分）
=$\frac{1}{3}×\frac{1}{2}×AC×OB×\frac{PO}{2}$=$\frac{1}{6}×4\sqrt{3}×2×\sqrt{3}=4$． …（14分）

点评 本题考查直线与平面平行与垂直的判定定理以及性质定理的应用，几何体的体积的求法，转化思想的应用，考查空间想象能力以及计算能力．