题目内容
7. 如图,在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹是椭圆,那么这个椭圆的离心率是( )
如图,在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹是椭圆,那么这个椭圆的离心率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 利用已知条件求出椭圆的方程,然后利用椭圆的离心率即可.
解答 解:设M(x,y),则P(x,2y),代入圆的方程并化简得:$\frac{{x}^{2}}{4}+{y}^{2}=1$,
解得a=2,b=1,c=$\sqrt{3}$.
椭圆的离心率为:$\frac{\sqrt{3}}{2}$.
故选:D.
点评 本题考查轨迹方程的求法,椭圆的简单性质的应用,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.在复平面内,复数z=(1+i)(2-i)对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
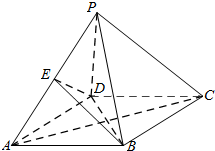 如图,四棱锥P-ABCD中,底面ABCD是边长为 4的菱形,PD=PB=4,∠BAD=60°,E为PA中点.
如图,四棱锥P-ABCD中,底面ABCD是边长为 4的菱形,PD=PB=4,∠BAD=60°,E为PA中点.