题目内容
2.定义在R上的奇函数f(x)满足当x≥0时,f(x)=log2(x+2)+(a-1)x+b(a,b为常数),若f(2)=-1,则f(-6)的值为4.分析 根据定义在R上的奇函数f(0)=0,求出b值,利用f(2)=-1,求出a,再由f(-6)=-f(6)得到答案.
解答 解:∵函数f(x)为定义在R上的奇函数,
∴f(0)=1+b=0,
解得:b=-1,
∴当x≥0时,f(x)=log2(x+2)+(a-1)x-1,
∵f(2)=-1,
∴f(2)=2+2(a-1)-1=-1,
∴a=0
∴f(x)=log2(x+2)-x-1,
∴f(-6)=-f(6)=4.
故答案为:4.
点评 本题考查的知识点是函数奇偶性的性质,熟练掌握函数奇偶性的定义和性质,是解答的关键.

练习册系列答案
相关题目
10.已知抛物线y2=-4$\sqrt{2}$x的焦点到双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=l(a>0,b>0)的一条渐近线的距离为$\frac{\sqrt{5}}{5}$,则该双曲线的离心率为( )
| A. | $\frac{2\sqrt{2}}{3}$ | B. | $\frac{\sqrt{10}}{3}$ | C. | $\sqrt{10}$ | D. | $\frac{2\sqrt{390}}{39}$ |
7.“a>b,c>0”是“ac>bc”的( )条件.
| A. | 必要不充分 | B. | 充分不必要 | ||
| C. | 充要 | D. | 既不充分也不必要 |
14.已知直线1:y=kx+$\frac{1}{2}$与离心率为e的双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,0<b<$\frac{1}{2}$)相交于A(x1,y1),B(x2,y2)两点,若对任意的k∈R,x1x2+y1y2恒为定值,则有( )
| A. | e2=$\frac{2}{1-4{b}^{2}}$ | B. | e2=$\frac{1}{1-4{b}^{2}}$ | C. | e2=$\frac{1+4{b}^{2}}{1-4{b}^{2}}$ | D. | e2=1-4b2 |
11.已知x>0,y>0,且$\frac{1}{x}+\frac{2}{y}$=1,若2x+y>t2+2t恒成立,则实数t的取值范围是( )
| A. | [-4,2] | B. | (-4,2) | C. | (0,2) | D. | (0,4) |
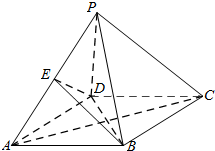 如图,四棱锥P-ABCD中,底面ABCD是边长为 4的菱形,PD=PB=4,∠BAD=60°,E为PA中点.
如图,四棱锥P-ABCD中,底面ABCD是边长为 4的菱形,PD=PB=4,∠BAD=60°,E为PA中点.