题目内容
8．已知i是虚数单位，则|$\frac{2i}{1+i}$|=（ ）| A． | 1 | B． | 2$\sqrt{2}$ | C． | 2 | D． | $\sqrt{2}$ |
分析 直接由复数代数形式的乘除运算化简，再由复数求模公式计算得答案．
解答 解：$\frac{2i}{1+i}$=$\frac{2i（1-i）}{（1+i）（1-i）}=1+i$，
则|$\frac{2i}{1+i}$|=$\sqrt{2}$．
故选：D．
点评 本题考查了复数代数形式的乘除运算，考查了复数模的求法，是基础题．
练习册系列答案
相关题目
18．已知函数$f（x）=\left\{\begin{array}{l}2-{log_2}（-x+2），0≤x＜2\\ 2-f（-x），-2＜x＜0\end{array}\right.$则|f（x）|≤2的解集为（ ）
| A． | [0，1] | B． | （-2，1] | C． | $[-\frac{7}{4}，2）$ | D． | $[{-\frac{7}{4}，1}]$ |
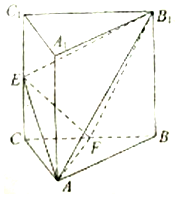如图，三棱柱ABC-A1B1C1中，侧棱AA1⊥平面ABC，△ABC为等腰直角三角形，∠BAC=90°，E，F分别是CC1，BC的中点，且AB=AA1．
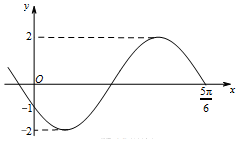已知函数y=Asin（ωx+φ）（A＞0，ω＞0，-π＜φ＜0）的部分图象如图所示，则φ=$-\frac{5π}{6}$．
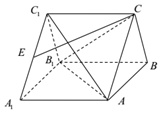如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，E为A1C1的中点，$\frac{{C{C_1}}}{{{C_1}E}}=\sqrt{2}$
18．已知角α的终边与单位圆x2+y2=1的交点为$P\;（x\;，\frac{{\sqrt{3}}}{2}）$，则cos2α=（ ）
| A． | $\frac{1}{2}$ | B． | $-\frac{1}{2}$ | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | 1 |