题目内容
7.设直线l过双曲线C的一个焦点,且与C的一条对称轴垂直,l与C交于A,B两点,|AB|为C的实轴长的2倍,则C的离心率为$\sqrt{3}$.分析 设双曲线方程,由题意可得丨AB丨=$\frac{2{b}^{2}}{a}$=2×2a,求得b2=2a2,根据双曲线的离心率公式e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$,即可求得C的离心率.
解答 解:设双曲线方程:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0),
由题意可知,将x=c代入,解得:y=±$\frac{{b}^{2}}{a}$,
则丨AB丨=$\frac{2{b}^{2}}{a}$,
由丨AB丨=2×2a,
则b2=2a2,
∴双曲线离心率e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题考查双曲线的简单几何性质,考查双曲线通径的求法,考查计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.已知集合A={0,1,2,3,4},B={x|x2-2x>0},则A∩B=( )
| A. | (2,4] | B. | [2,4] | C. | {0,3,4} | D. | {3,4} |
12.已知$\overrightarrow a=({1,cosa}),\overrightarrow b=({sina,1})$,若$\overrightarrow a⊥\overrightarrow b$,则sin2α=( )
| A. | $-\frac{1}{2}$ | B. | -1 | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
19.设F为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的右焦点,若OF的垂直平分线与渐近线在第一象限内的交点到另一条渐近线的距离为$\frac{1}{2}|OF|$,则双曲线的离心率为( )
| A. | $2\sqrt{2}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $2\sqrt{3}$ | D. | 3 |
16.定义在R上的偶函数f(x)满足:对任意的x1,x2∈(-∞,0)(x1≠x2),有$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<0,则( )
| A. | f(-3)<f(-2)<f(1) | B. | f(1)<f(-2)<f(-3) | C. | f(-2)<f(1)<f(-3) | D. | f(-3)<f(1)<f(-2) |
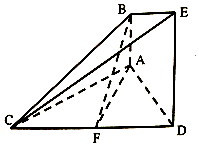 如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.
如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.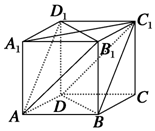 在正方体ABCD-A1B1C1D1中,如图.
在正方体ABCD-A1B1C1D1中,如图.