题目内容
3．数轴上点A，B分别对应-1、2，则向量$\overrightarrow{AB}$的长度是（ ）| A． | -1 | B． | 2 | C． | 1 | D． | 3 |
分析 求出线段AB的长，从而求出向量$\overrightarrow{AB}$的模即可．
解答 解：数轴上点A，B分别对应-1、2，
则向量$\overrightarrow{AB}$的长度即|$\overrightarrow{AB}$|=3，
故选：D．
点评 本题考查了向量求模问题，是一道基础题．
练习册系列答案
相关题目
13．阅读如图所示的程序框图，若输入$a=\frac{10}{21}$，则输出的k值是（ ）
| A． | 9 | B． | 10 | C． | 11 | D． | 12 |
11．设f（x）是定义在R上的偶函数，且f（2+x）=f（2-x），当x∈[-2，0]时，$f（x）={（\frac{{\sqrt{2}}}{2}）^x}-1$，若在区间（-2，6）内关于x的方程f（x）-loga（x+2）=0（a＞0，a≠1），恰有3个不同的实数根，则实数a的取值范围是（ ）
| A． | $（\frac{1}{4}，1）$ | B． | （1，4） | C． | （4，8） | D． | （8，+∞） |
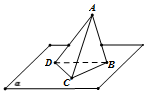如图，三棱锥A-BCD的顶点B、C、D在平面α内，CA=AB=BC=CD=DB=4，AD=2$\sqrt{6}$，若将该三棱锥以BC为轴转动，到点A落到平面α内为止，则A、D两点所经过的路程之和是 $2\sqrt{3}π$．