题目内容
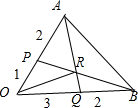
在△AOB的边OA、OB上分别有一点P、Q,已知OP:PA=1:2,OQ:QB=3:2,连结AQ、BP,设它们交于R点,若
=
,
=
,设
=λ
+μ
,试求出λ和μ的值.
| OA |
| a |
| OB |
| b |
| OR |
| a |
| b |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:想办法用
,
表示
,通过观察图形,可以发现有两种表示方式,根据向量的加法:一种是,
=
+
,
和
共线,所以存在实数x使
=x
=x(
-
),带入并整理得:
=
+(1-x)
;一种是
=
+
,同样的办法可求得
=(1-y)
+
,这时候可以建立关于x,y的方程组,解出x,y即可求出λ,μ.
| a |
| b |
| OR |
| OR |
| OA |
| AR |
| AR |
| AQ |
| AR |
| AQ |
| 3 |
| 5 |
| b |
| a |
| OR |
| x |
| 3 |
| a |
| b |
| OR |
| OB |
| BR |
| OR |
| a |
| 3y |
| 5 |
| b |
解答:
解:∵
和
共线,∴存在实数x使
=x
,同样,存在实数y使
=y
;
=
+
=
+x
=
+x(
-
)=
+(1-x)
;
=
+
=
+y
+y(
-
)=(1-y)
+
;
∴
+(1-x)
=(1-y)
+
;
∵
,
不共线;
∴
,解得x=
,y=
;
∴
=
+
;
∴λ=
,μ=
.
| AR |
| AQ |
| AR |
| AQ |
| BR |
| BP |
| OR |
| OB |
| BP |
| OB |
| BP |
| b |
| 1 |
| 3 |
| a |
| b |
| x |
| 3 |
| a |
| b |

| OR |
| OA |
| AR |
| OA |
| AQ |
| a |
| 3 |
| 5 |
| b |
| a |
| a |
| 3y |
| 5 |
| b |
∴
| x |
| 3 |
| a |
| b |
| a |
| 3y |
| 5 |
| b |
∵
| a |
| b |
∴
|
| 1 |
| 2 |
| 5 |
| 6 |
∴
| OR |
| 1 |
| 6 |
| a |
| 1 |
| 2 |
| b |
∴λ=
| 1 |
| 6 |
| 1 |
| 2 |
点评:考查向量的加法运算,共线向量基本定理,共面向量基本定理,用两种方式表示
是求解本题的关键.
| OR |

练习册系列答案
相关题目