题目内容
点(1,2)在圆
的( )
|
| A、内部 | B、外部 |
| C、圆上 | D、与θ的值有关 |
考点:圆的参数方程
专题:计算题,坐标系和参数方程
分析:圆
,化为普通方程,(1,2)代入左边可得(x+1)2+y2=8<64,即可得出结论.
|
解答:
解:圆
,化为普通方程为(x+1)2+y2=64,
(1,2)代入左边可得(x+1)2+y2=8<64.
故选:A.
|
(1,2)代入左边可得(x+1)2+y2=8<64.
故选:A.
点评:本题考查圆的参数方程,考查点与圆的位置关系,考查学生的计算能力,属于基础题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
已知直线l1:4x-3y+11=0和直线l2:x+1=0,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值为( )
| A、2 | ||
| B、3 | ||
C、
| ||
D、
|
若x是纯虚数,y是实数,且2x-1+i=y-(3-y)i,则x+y等于( )
A、1+
| ||
B、-1+
| ||
C、1-
| ||
D、-1-
|
设复数z满足z(a+i)=1+i,若复数z为纯虚数,则实数a=( )
| A、-1 | B、1 | C、-2 | D、2 |
已知整数的数对列如下:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4),…则第60个数对是( )
| A、(3,8) |
| B、(4,7) |
| C、(4,8) |
| D、(5,7) |
扇形的周长是16,圆心角是2rad,则扇形的面积是( )
| A、16 | B、32 |
| C、16π | D、32π |
已知复数z=i(2+i),则它的共轭复数在复平面内对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知命题p:“?x∈R,?m∈R,使4x+2x•m+1=0”.若命题p为真命题,则实数m的取值范围是( )
| A、(-∞,-2] |
| B、[2,+∞) |
| C、(-∞,-2) |
| D、(2,+∞) |
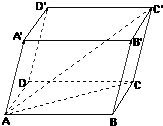 如图在平行六面体ABCD-A′B′C′D′中,AB=4,AD=3,AA′=5,∠BAD=90°,∠BAA′=∠DAA′=60°,则AC′的长是
如图在平行六面体ABCD-A′B′C′D′中,AB=4,AD=3,AA′=5,∠BAD=90°,∠BAA′=∠DAA′=60°,则AC′的长是