题目内容
极点到直线ρ(cosθ-sinθ)=2的距离为 .
考点:简单曲线的极坐标方程
专题:计算题,坐标系和参数方程
分析:先将原极坐标方程化成直角坐标方程,再利用直角坐标方程点到直线的距离进行求解即可.
解答:
解:将原极坐标方程ρ(cosθ-sinθ)=2化为:直角坐标方程为:x-y=2,
原点到该直线的距离是:
=
.
∴所求的距离是:
.
故答案为:
.
原点到该直线的距离是:
| 2 | ||
|
| 2 |
∴所求的距离是:
| 2 |
故答案为:
| 2 |
点评:本题考查点的极坐标和直角坐标的互化,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知直线l1:4x-3y+11=0和直线l2:x+1=0,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值为( )
| A、2 | ||
| B、3 | ||
C、
| ||
D、
|
 如图,在Rt△ABC中,AB=BC,以AB为直径的⊙O交AC于D,过D作DE⊥BC,垂足为E,连接AE交⊙O于点F,求证:CE2=EF•EA.
如图,在Rt△ABC中,AB=BC,以AB为直径的⊙O交AC于D,过D作DE⊥BC,垂足为E,连接AE交⊙O于点F,求证:CE2=EF•EA.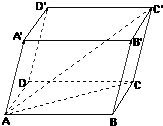 如图在平行六面体ABCD-A′B′C′D′中,AB=4,AD=3,AA′=5,∠BAD=90°,∠BAA′=∠DAA′=60°,则AC′的长是
如图在平行六面体ABCD-A′B′C′D′中,AB=4,AD=3,AA′=5,∠BAD=90°,∠BAA′=∠DAA′=60°,则AC′的长是