题目内容
12.已知长方形ABCD如图1中,AD=$\sqrt{3}$,AB=2,E为AB中点,将△ADE沿DE折起到△PDE,所得四棱锥P-BCDE如图2所示.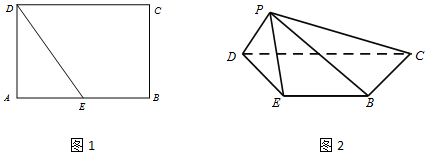
(Ⅰ)若点M为PC中点,求证:BM∥平面PDE;
(Ⅱ)当平面PDE⊥平面BCDE时,求三棱锥E-PCD的体积.
分析 (Ⅰ)取DP中点F,连结EF、FM,推导出FEBM是平行四边形,从而BM∥EF,由此能证明BM∥平面PDE.
(Ⅱ)过P作PH⊥DE于H,则PH⊥平面EBCD,三棱锥E-PCD的体积VE-PCD=VP-DEC,由此能求出结果.
解答 证明:(Ⅰ)取DP中点F,连结EF、FM,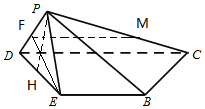
∵△PDC中,点F、M分别是DP、PC的中点,
∴FM$\underset{∥}{=}$$\frac{1}{2}$DC,又EB$\underset{∥}{=}$$\frac{1}{2}$DC,
∴FM$\underset{∥}{=}$EB,∴FEBM是平行四边形,∴BM∥EF,
又EF?平面PDE,BM?平面PDE,
∴BM∥平面PDE.
解:(Ⅱ)∵平面PDE⊥平面EBCD,且平面PDE∩平面EBCD=DE,
过P作PH⊥DE于H,∴PH⊥平面EBCD,
在Rt△PDE中,过P作PH⊥DE于H,∴PH⊥平面EBCD,
在Rt△PDE中,由题意得PH=$\frac{\sqrt{3}}{2}$,
在Rt△DEC中,DE=$\sqrt{(\sqrt{3})^{2}+{{1}^{2}}_{\;}}$=2,且DE=EC=2,
∴${S}_{△DEC}=\frac{1}{2}×2×2×\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴三棱锥E-PCD的体积VE-PCD=VP-DEC=$\frac{1}{3}×{S}_{△DEC}×PH$=$\frac{1}{3}×\sqrt{3}×\frac{\sqrt{3}}{2}$=$\frac{1}{2}$.
点评 本题考查线面平行的证明,考查几何体的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想、函数与方程思想,是中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (1,6) | B. | (1,5) | C. | (3,6) | D. | (3,5) |
| A. | $\frac{3+\sqrt{3}+2\sqrt{2}}{2}$ | B. | $\frac{1+\sqrt{3}+\sqrt{2}}{2}$ | C. | $\frac{1+\sqrt{3}+2\sqrt{2}}{2}$ | D. | $\frac{3}{2}$+2$\sqrt{2}$ |
| A. | $8\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $\frac{8\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
| A. | y=-x3 | B. | y=2|x| | C. | y=${x}^{\frac{1}{2}}$ | D. | y=log3(-x) |
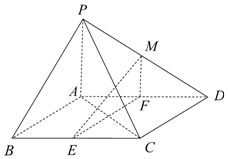 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上.