题目内容
1．若a满足方程xex=4，b满足方程xlnx=4，则函数f（x）=log${\;}_{\sqrt{ab}}$（x+4）-（ab）x（ ）| A． | 仅有一个或没有零点 | B． | 有两个正零点 | ||
| C． | 有一个正零点和一个负零点 | D． | 有两个负零点 |
分析 作出y=ex，y=lnx，y=$\frac{4}{x}$的函数图象，根据三个函数的对称关系得出ab=4，再作出y=log2（x+4）与y=4x的函数图象，根据图象判断结论．
解答 解：作出y=ex，y=lnx，y=$\frac{4}{x}$的函数图象，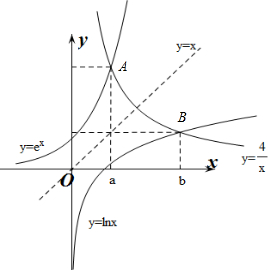
设A（a，$\frac{4}{a}$），B（b，$\frac{4}{b}$），
∵y=lnx与y=ex关于直线y=x对称，y=$\frac{4}{x}$关于直线y=x对称，
∴A，B关于直线y=x对称，∴$\left\{\begin{array}{l}{a=\frac{4}{b}}\\{b=\frac{4}{a}}\end{array}\right.$，即ab=4．
∴f（x）=log2（x+4）-4x，
作出y=log2（x+4）与y=4x的函数图象，如图所示：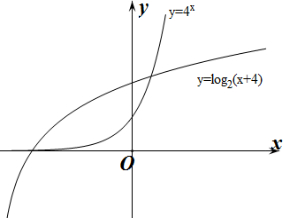
由图象可知f（x）有一正一负两个零点．
故选C．
点评 本题考查了函数零点与函数图象的关系，属于中档题．
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
9．若全集U=R，集合A={x|-1≤x＜1}，B={x|x≤0或x＞2}，则集合A∪∁UB=（ ）
| A． | {x|0＜x＜1} | B． | {x|-1≤x≤2} | C． | {x|-1＜x＜2} | D． | {x|0≤x≤1} |
16．已知函数f（x）对任意的x∈R，都有f（-x）+f（x）=-6，且当x≥0时，f（x）=2x-4，定义在R上的函数g（x）=a（x-a）（x+a+1），两函数同时满足：?x∈R，都有f（x）＜0或g（x）＜0；?x∈（-∞，-1），f（x）•g（x）＜0，则实数a的取值范围为（ ）
| A． | （-3，0） | B． | $（-3，-\frac{1}{2}）$ | C． | （-3，-1） | D． | （-3，-1] |
13．某初级中学篮球队假期集训，集训前共有8个篮球，其中4个是新的（即没有用过的球），4个是旧的（即至少用过一次的球），毎次训练都从中任意取出2个球，用完后放回，则第二次训练时恰好取到1个新球的概率为（ ）
| A． | $\frac{24}{49}$ | B． | $\frac{4}{7}$ | C． | $\frac{25}{49}$ | D． | $\frac{51}{98}$ |