题目内容
12.某公司准备将1000万元资金投入到市环保工程建设中,现有甲、乙两个建设项目选择,若投资甲项目一年后可获得的利润ξ1(万元)的概率分布列如表所示:| ξ1 | 110 | 120 | 170 |
| P | m | 0.4 | n |
| X | 0 | 1 | 2 |
| ξ2 | 41.2 | 117.6 | 204.0 |
(Ⅱ)求ξ2的分布列;
(Ⅲ)若该公司投资乙项目一年后能获得较多的利润,求p的取值范围.
分析 (Ⅰ)由离散型随机变量的分布列及数学期望的性质列出方程组,能求出m,n的值.
(Ⅱ)ξ2的可能取值为41.2,117.6,204,分虽求出相应的概率,由此能求出ξ2的分布列.
(Ⅲ)求出可得E(ξ2),由于该公司投资乙项目一年后能获得较多的利润,从而E(ξ2)>E(ξ1),由此能求出p的取值范围.
解答 解:(Ⅰ)由题意得$\left\{\begin{array}{l}m+0.4+n=1\\ 110m+120×0.4+170n=120\end{array}\right.$,
解得m=0.5,n=0.1.
(Ⅱ)ξ2的可能取值为41.2,117.6,204,
P(ξ2=41.2)=(1-p)[1-(1-p)]=p(1-p),
$P({ξ_2}=117.6)=p[{1-(1-p)}]+(1-p)(1-p)={p^2}+{(1-p)^2}$,
P(ξ2=204)=p(1-p),
所以ξ2的分布列为:
| ξ2 | 41.2 | 117.6 | 204 |
| P | p(1-p) | p2+(1-p)2 | p(1-p) |
由于该公司投资乙项目一年后能获得较多的利润,
所以E(ξ2)>E(ξ1),
所以-10p2+10p+117.6>120,
解得0.4<p<0.6,所以p的取值范围是(0.4,0.6).
点评 本题考查离散型随机变量的分布列及数学期望的求法及应用,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.

练习册系列答案
相关题目
2.已知函数f(x)=(2017x-$\frac{1}{201{7}^{x}}$)x2017,若f(log2a)+f(log0.5a)≤$\frac{2(201{7}^{2}-1)}{2017}$,则实数a的取值范围是( )
| A. | (0,2] | B. | (0,$\frac{2}{3}$]∪[1,+∞) | C. | (0,$\frac{1}{2}$]∪[2,+∞) | D. | [$\frac{1}{2}$,2] |
3.设$\frac{i}{1+i}$=a+bi(a,b∈R,i为虚数单位),则|a-bi|=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
17.若将函数y=sin2x的图象向左平移$\frac{π}{6}$个单位,则平移后的图象( )
| A. | 关于点$(-\frac{π}{12},0)$对称 | B. | 关于直线$x=-\frac{π}{12}$对称 | ||
| C. | 关于点$(\frac{π}{12},0)$对称 | D. | 关于直线$x=\frac{π}{12}$对称 |
1.五个人负责一个社团的周一至周五的值班工作,每人一天,则甲同学不值周一,乙同学不值周五,且甲,乙不相邻的概率是( )
| A. | $\frac{3}{10}$ | B. | $\frac{7}{20}$ | C. | $\frac{2}{5}$ | D. | $\frac{13}{30}$ |
2.命题“若a>b,则a+c>b+c”的逆命题是( )
| A. | 若a>b,则a+c≤b+c | B. | 若a+c≤b+c,则a≤b | C. | 若a+c>b+c,则a>b | D. | 若a≤b,则a+c≤b+c |
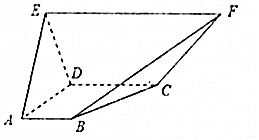 在如图所示的五面体中,面ABCD为直角梯形,∠BAD=∠ADC=$\frac{π}{2}$,平面ADE⊥平面ABCD,EF=2DC=4AB=4,△ADE是边长为2的正三角形.
在如图所示的五面体中,面ABCD为直角梯形,∠BAD=∠ADC=$\frac{π}{2}$,平面ADE⊥平面ABCD,EF=2DC=4AB=4,△ADE是边长为2的正三角形.