题目内容
19.满足42x-1>($\frac{1}{2}$)-x-4的实数x的取值范围为(2,+∞).分析 根据指数函数的定义和性质,把不等式化为2(2x-1)>x+4,求出解集即可.
解答 解:不等式42x-1>($\frac{1}{2}$)-x-4可化为
22(2x-1)>2x+4,
即2(2x-1)>x+4,
解得x>2,
所以实数x的取值范围是(2,+∞).
故选:(2,+∞).
点评 本题考查了指数函数不等式的解法与应用问题,是基础题目.

练习册系列答案
相关题目
10.如果a<b<0,则下列不等式成立的是( )
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | a-c<b-c | C. | ac2<bc2 | D. | a2<b2 |
7.集合A={x∈N+|-1<x<4},B={x|x2≤4},则A∩B=( )
| A. | {0,1,2} | B. | {1,2} | C. | {1,2,3} | D. | {0,1,2,3} |
14.已知函数f(x)=$\frac{\sqrt{5-ax}}{a-2}$(a∈A),若f(x)在区间(0,1]上是减函数,则集合A可以是( )
| A. | (-∞,0) | B. | [1,2) | C. | (-1,5] | D. | [4,6] |
11.已知θ∈(0,π),tanθ=-$\frac{3}{2}$,则cosθ=( )
| A. | $\frac{3}{{\sqrt{13}}}$ | B. | $-\frac{2}{{\sqrt{13}}}$ | C. | $\frac{2}{{\sqrt{13}}}$ | D. | $-\frac{3}{{\sqrt{13}}}$ |
9.在长方体ABCD-A1B1C1D1中,AB=BC=4,AA1=2,则直线BC1与平面BB1D1D所成角的正弦值为( )
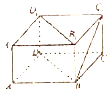

| A. | $\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{2\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{15}}}{5}$ | D. | $\frac{{\sqrt{10}}}{5}$ |