题目内容
11.已知θ∈(0,π),tanθ=-$\frac{3}{2}$,则cosθ=( )| A. | $\frac{3}{{\sqrt{13}}}$ | B. | $-\frac{2}{{\sqrt{13}}}$ | C. | $\frac{2}{{\sqrt{13}}}$ | D. | $-\frac{3}{{\sqrt{13}}}$ |
分析 利用同角三角函数基本关系式化简求解即可.
解答 解:θ∈(0,π),tanθ=$\frac{sinθ}{cosθ}$=-$\frac{3}{2}$,∴θ为钝角,又sin2θ+cos2θ=1,
则cosθ=-$\frac{2}{\sqrt{13}}$,
故选:B.
点评 本题主要考查同角三角函数的基本关系,以及三角函数在各个象限中的符号,属于基础题.

练习册系列答案
相关题目
1.已知直线y=ax是曲线y=lnx的切线,则实数a=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2e}$ | C. | $\frac{1}{e}$ | D. | $\frac{1}{{e}^{2}}$ |
16.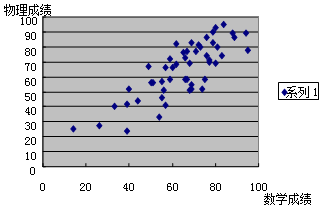 在调查分析某班级数学成绩与物理成绩的相关关系时,对数据进行统计分析得到如下散点图,用回归直线$\hat y=bx+a$近似刻画其关系,根据图形,b的数值最有可能是( )
在调查分析某班级数学成绩与物理成绩的相关关系时,对数据进行统计分析得到如下散点图,用回归直线$\hat y=bx+a$近似刻画其关系,根据图形,b的数值最有可能是( )
 在调查分析某班级数学成绩与物理成绩的相关关系时,对数据进行统计分析得到如下散点图,用回归直线$\hat y=bx+a$近似刻画其关系,根据图形,b的数值最有可能是( )
在调查分析某班级数学成绩与物理成绩的相关关系时,对数据进行统计分析得到如下散点图,用回归直线$\hat y=bx+a$近似刻画其关系,根据图形,b的数值最有可能是( )| A. | 0 | B. | 1.55 | C. | 0.45 | D. | -0.24 |