题目内容
5.在△ABC中,已知a2=b(b+c),则$\frac{A}{B}$=2.分析 由已知式子和正弦定理可得sin2A-sin2B=sinBsinC,分解因式由和差化积公式化简可得sin(A-B)=sinB,再由三角形的内角和可得.
解答 解:∵在△ABC中a2=b(b+c),∴a2-b2=bc,
∴由正弦定理可得sin2A-sin2B=sinBsinC,
∴(sinA+sinB)(sinA-sinB)=sinBsinC,
由和差化积公式可得2sin$\frac{A+B}{2}$cos$\frac{A-B}{2}$•2cos$\frac{A+B}{2}$sin$\frac{A-B}{2}$=sinBsinC,
∴2sin$\frac{A+B}{2}$cos$\frac{A+B}{2}$•2cos$\frac{A-B}{2}$•sin$\frac{A-B}{2}$=sinBsinC,
∴sin(A+B)sin(A-B)=sinBsinC,即sinCsin(A-B)=sinBsinC,
约掉sinC可得sin(A-B)=sinB,可得A-B=B,
故可得A=2B,∴$\frac{A}{B}$=2,
故答案为:2.
点评 本题考查正余弦定理三角形,涉及和差化积公式和三角形的内角和,属中档题.

练习册系列答案
相关题目
16.在△ABC内,若$bsinA=\sqrt{3}acosB$,b=3,sinC=2sinA,则c的值为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $3\sqrt{3}$ |
14.已知sinθ-2cosθ=0,则cos2θ-sin2θ=( )
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
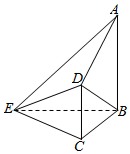 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=$\frac{2π}{3}$.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=$\frac{2π}{3}$.