题目内容
8．
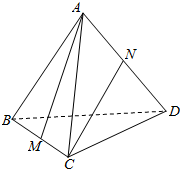在正四面体（四个面都是正三角形的四面体是正四面体）中，M，N分别是BC和AD的中点，试作出异面直线AM与CN所成角．
分析 连结MD，取MD的中点O，连结NO，CO，则∠CNO是异面直线AM与CN所成角．
解答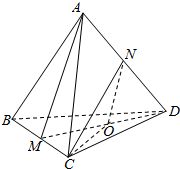 
解：连结MD，取MD的中点O，连结NO，CO，
∵正四面体（四个面都是正三角形的四面体是正四面体）中，M，N分别是BC和AD的中点，
∴NO∥AM，∴∠CNO是异面直线AM与CN所成角，
设正四面体A-BCD的棱长为2，
则AM=CN=DM=$\sqrt{4-1}$=$\sqrt{3}$，ON=$\frac{AM}{2}$=$\frac{\sqrt{3}}{2}$，OM=$\frac{DM}{2}$=$\frac{\sqrt{3}}{2}$，
OC=$\sqrt{1+\frac{3}{4}}$=$\frac{\sqrt{7}}{2}$，
∴cos∠CNO=$\frac{C{N}^{2}+O{N}^{2}-C{O}^{2}}{2CN•ON}$=$\frac{3+\frac{3}{4}-\frac{7}{4}}{2×\sqrt{3}×\frac{\sqrt{3}}{2}}$=$\frac{2}{3}$．
∴异面直线AM与CN所成角∠CNO=arccos$\frac{2}{3}$．
点评 本题考查异面直线所成角的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
阅读快车系列答案
相关题目
16．在△ABC内，若$bsinA=\sqrt{3}acosB$，b=3，sinC=2sinA，则c的值为（ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $\sqrt{3}$ | C． | $2\sqrt{3}$ | D． | $3\sqrt{3}$ |
3．
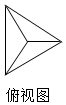一个正四面体的体积为$\frac{2\sqrt{2}}{3}$，它的三视图中的俯视图如图所示（其中三个小三角形全等），侧视图是一个三角形，则这个三角形的面积是（ ）
一个正四面体的体积为$\frac{2\sqrt{2}}{3}$，它的三视图中的俯视图如图所示（其中三个小三角形全等），侧视图是一个三角形，则这个三角形的面积是（ ）| A． | $\frac{\sqrt{6}}{3}$ | B． | $\frac{2\sqrt{6}}{3}$ | C． | $\frac{2\sqrt{2}}{3}$ | D． | $\sqrt{3}$ |