题目内容
过原点且倾斜角为60°的直线与圆：x2+y2-4y=0的位置关系是（ ）
| A、相切 | B、相交 |
| C、相离 | D、无法确定 |
考点：直线与圆的位置关系
专题：计算题,直线与圆
分析：求出直线的方程为y=
x，化简圆方程得圆心为（0，2）且半径r=2．利用点到直线的距离公式算出圆心到直线的距离，即可判断直线与圆的位置关系．
| 3 |
解答：
解：∵直线的倾斜角为60°，∴直线的斜率k=tan60°=
，
结合直线过原点，得直线方程为y=
x，即
x-y=0
∵圆x2+y2-4y=0，即x2+（y-2）2=4，
得圆心为（0，2），半径r=2．
∴圆心到直线的距离d=
=1＜2，
∴直线与圆：x2+y2-4y=0的位置关系是：相交．
故选：B．
| 3 |
结合直线过原点，得直线方程为y=
| 3 |
| 3 |
∵圆x2+y2-4y=0，即x2+（y-2）2=4，
得圆心为（0，2），半径r=2．
∴圆心到直线的距离d=
| |-2| | ||||
|
∴直线与圆：x2+y2-4y=0的位置关系是：相交．
故选：B．
点评：本题考查直线与圆的位置关系，求点到直线的距离公式的应用．属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
已知箱中共有6个球，其中红球、黄球、蓝球各2个．每次从该箱中取1个球 （有放回，每球取到的机会均等），共取三次．设事件A：“第一次取到的球和第二次取到的球颜色相同”，事件B：“三次取到的球颜色都相同”，则P（B|A）=（ ）
A、
| ||
B、
| ||
C、
| ||
| D、1 |
在△ABC中，已知sinA=sinBcosC，则该三角形的形状是（ ）
| A、等边三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、等腰直角三角形 |
不等式
＜0的解集为（ ）
| x2 |
| x+1 |
| A、（-1，0）∪（0，+∞） |
| B、（-∞，-1）∪（0，1） |
| C、（-1，0） |
| D、（-∞，-1） |
若直线l的方向向量为（-1，2），则直线l的斜率是（ ）
| A、-2 | ||
| B、2 | ||
C、
| ||
D、-
|
下列各式中正确的是（ ）
（1）（λ•
）•
=λ•（
）=
•（λ
）
（2）|
•
|=|
|•|
|
（3）（
•
）•
=
•（
•
）
（4）（
+
）•
=
•
+
•
．
（1）（λ•
| a |
| b |
| a |
| b |
| a |
| b |
（2）|
| a |
| b |
| a |
| b |
（3）（
| a |
| b |
| c |
| a |
| b |
| c |
（4）（
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| A、（1）（3） |
| B、（2）（4） |
| C、（1）（4） |
| D、以上都不对 |
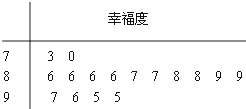前不久，省社科院发布了2013年度“安徽城市居民幸福排行榜”，芜湖市成为本年度安徽最“幸福城”．随后，师大附中学生会组织部分同学，用“10分制”随机调查“阳光”社区人们的幸福度．现从调查人群中随机抽取16名，如图所示的茎叶图记录了他们的幸福度分数（以小数点前的一位数字为茎，小数点后的一位数字为叶）：