题目内容
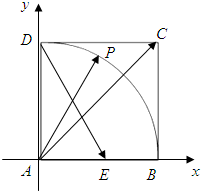
在正方形ABCD中,E为AB的中点P是A为圆心,AB为半径的圆弧
上的任意一点.
(1)若向正方形ABCD内撒一枚幸运小花朵,则小花朵落在扇形ABD内的概率为 ;
(2)设∠PAB=θ,向量
=λ
+μ
(λ,μ∈R),若μ-λ=1,则θ= .
 |
| BD |
(1)若向正方形ABCD内撒一枚幸运小花朵,则小花朵落在扇形ABD内的概率为
(2)设∠PAB=θ,向量
| AC |
| DE |
| AP |
考点:几何概型
专题:概率与统计
分析:(1)利用几何概型,所求概率为扇形ABD与正方形ABCD比值;
(2)不妨设正方形边长为1以A坐标原点,AB,AD线为x轴,y建立直角坐标系,将相关向量用坐标表示,利用向量相等得到用θ表示的λ,μ的方程组解之.
(2)不妨设正方形边长为1以A坐标原点,AB,AD线为x轴,y建立直角坐标系,将相关向量用坐标表示,利用向量相等得到用θ表示的λ,μ的方程组解之.
解答:
 解:(1)所求概率为扇形ABD与正方形ABCD比值,设正方形边长为a,所求概率为P=
解:(1)所求概率为扇形ABD与正方形ABCD比值,设正方形边长为a,所求概率为P=
=
;
(2)不妨设正方形边长为1以A坐标原点,AB
AD线为x轴,y建立直角坐标系,则
=(
,-1),
=(1,1),
=(cosθ,sinθ),
=λ
+μ
,
,所以
,所以μ-λ=1,sinθ=1,θ=
;
故答案为:
,
.
 解:(1)所求概率为扇形ABD与正方形ABCD比值,设正方形边长为a,所求概率为P=
解:(1)所求概率为扇形ABD与正方形ABCD比值,设正方形边长为a,所求概率为P=
| ||
| a2 |
| π |
| 4 |
(2)不妨设正方形边长为1以A坐标原点,AB
AD线为x轴,y建立直角坐标系,则
| DE |
| 1 |
| 2 |
| AC |
| AP |
| AC |
| DE |
| AP |
|
|
| π |
| 2 |
故答案为:
| π |
| 4 |
| π |
| 2 |
点评:本题是一道涉及几何概型和向量知识的综合问题.第(1)题是几何概型问题,求解转化为扇形的面积与正方形面积的比来解决;第(2)问是关于平面向量线性运算的考题,解题时可建立适当的坐标系,用向量的坐标运算来实现转化.若假设正方形边长为1,则点P单位圆上,就可以考虑引入三角函数来表示点P坐

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
已知函数f(x)=sin(x-φ)-1(0<φ<
),且
(f(x)+1)dx=0,则函数f(x)的一个零点是( )
| π |
| 2 |
| ∫ |
0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知A,B两地相距150km,某人驾驶汽车以60km/h的速度从A地到达B地,在B地停留1h后再以50km/h的速度返回A地并停在A地,将汽车与A地的距离s(单位:km)表示成时间t(单位:h)的函数为( )
| A、s=60t | |||||||||||
B、s=
| |||||||||||
C、s=
| |||||||||||
| D、s=60t+50 |