题目内容
已知A，B两地相距150km，某人驾驶汽车以60km/h的速度从A地到达B地，在B地停留1h后再以50km/h的速度返回A地并停在A地，将汽车与A地的距离s（单位：km）表示成时间t（单位：h）的函数为（ ）
| A、s=60t | |||||||||||
B、s=
| |||||||||||
C、s=
| |||||||||||
| D、s=60t+50 |
考点：函数解析式的求解及常用方法
专题：应用题,函数的性质及应用
分析：根据题意，计算汽车与A地的距离s与时间t的函数关系即可．
解答：
解：根据题意，得；
=2.5，
=3；
∴当0≤t≤2.5时，s=60t，
当2.5＜t≤3.5时，s=150，
当3.5＜t≤6.5时，s=150-50（t-3.5），
当t＞6.5时，s=0；
∴路程与时间的关系是
s=
．
故选：B．
| 150 |
| 60 |
| 150 |
| 50 |
∴当0≤t≤2.5时，s=60t，
当2.5＜t≤3.5时，s=150，
当3.5＜t≤6.5时，s=150-50（t-3.5），
当t＞6.5时，s=0；
∴路程与时间的关系是
s=
|
故选：B．
点评：本题考查了路程s与时间t的函数关系的应用问题，也考查了分段函数的应用问题，是基础题目．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
已知复数z=
，则|z|=（ ）
| 1 |
| i(i+1) |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知
=（sinα，cosα），
=（-2，1），若
⊥
，则tanα的值为（ ）
| a |
| b |
| a |
| b |
| A、-2 | ||
| B、2 | ||
C、
| ||
D、-
|
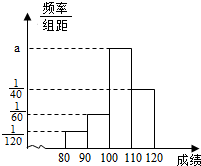某校从参加某次数学能力测试的学生中中抽查36名学生，统计了他们的数学成绩（成绩均为整数且满分为120分），成绩的频率直方图如图所示，